Question

Write the expression for a rational function that has a horizontal asymptote along the line y=3/4, exactly two zeros, exactly one hole, and exactly two vertical asymptotes. Leave your answer in factored form.

Answer 1

`f(x)=(3(x-3)(x-4)(x-5))/(4(x-1)(x-2)(x-3))`

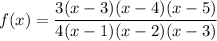
Explanation:

A rational function is a mathematical function that can be expressed as the ratio of two polynomials:

`f(x)=(p(x))/(q(x))`

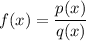
Vertical asymptotes occur at the x-values where the denominator of a rational function equals zero. Therefore, for the rational function to have two vertical asymptotes, configure the denominator in the form (x - a)(x - b):

`f(x)=(p(x))/((x-1)(x-2))`

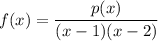
Therefore, this rational function will have vertical asymptotes at x = 1 and x = 2.

A removable discontinuity (hole) occurs when a rational function has a factor with an x that is in both the numerator and the denominator. Therefore, if the rational function has exactly one hole, we need to add a third factor to the denominator and duplicate this in the numerator:

`f(x)=((x-3))/((x-1)(x-2)(x-3))`

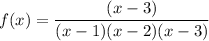
Therefore, this rational function has vertical asymptotes at x = 1 and x = 2, and a hole at x = 3.

Zeros occur at the x-values that make the numerator of a rational function equal to zero. Therefore, add two further (x - a) factors to the numerator that are different to the those in the numerator:

Zeros occur at the x-values where the numerator of a rational function equals zero. To introduce exactly two zeros, include two additional (x - a) factors in the numerator that are distinct from those already present in the function:

`f(x)=((x-3)(x-4)(x-5))/((x-1)(x-2)(x-3))`

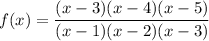
Therefore, this rational function has vertical asymptotes at x = 1 and x = 2, a hole at x = 3, and zeros at x = 4 and x = 5.

In a rational function where the polynomials of the numerator and denominator have the same highest degree term, the horizontal asymptote is found by dividing the coefficient of the highest-degree term in the numerator by the coefficient of the highest-degree term in the denominator. Therefore, for the rational function to have a horizontal asymptote at y = 3/4, multiply the numerator by 3 and the denominator by 4:

`f(x)=(3(x-3)(x-4)(x-5))/(4(x-1)(x-2)(x-3))`

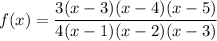
Therefore, this rational function has:

• A horizontal asymptote at y = 3/4.
• Exactly two zeros at x = 4 and x = 5.
• Exactly one hole at x = 3.
• Exactly two vertical asymptotes at x = 1 and x = 2.