Question

Find the equation of the linear function represented by the table below in slope-intercept form.

x y
-3 2
1 -2
5 -6
9 -10

Answer 1

y=-3x+2

y=1x-2

y=5x-6

y=9x-10

Explanation:

y=-3x+2

y=1x-2

y=5x-6

y=9x-10

To get the equation all you have to do is put the input and outputs into slope intercept form which is y=mx+b.

Answer 2

`y=-x-1`

Explanation:

To find the equation of the linear function represented by the given table, we first need to find its slope by using the slope formula.

`\boxed{\begin{array}{l}\underline{\textsf{Slope formula}}\\\\\large\text{$m=(y_2-y_1)/(x_2-x_1)$}\\\\\textsf{where:}\\\phantom{w}\bullet\;\;m\; \textsf{is the slope.}\\\phantom{w}\bullet\;\;(x_1,y_1)\;\textsf{and}\;(x_2,y_2)\;\textsf{are two points on the line.}\\\end{array}}`

Substitute two points from the table (-3, 2) and (1, -2) into the slope formula:

`m=(-2-2)/(1-(-3))=(-4)/(4)=-1`

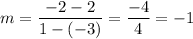
Therefore, the slope is m = -1.

The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. To find the value of b, substitute the found slope m = -1 and one of the points from the table (-3, 2) into the formula and solve for b:

`\begin{aligned}y&=mx+b\\2&=-1(-3)+b\\2&=3+b\\-1&=b\\b&=-1\end{aligned}`

Therefore, the y-intercept is b = -1.

Finally, to find the equation of the linear function represented by the given table, substitute m = -1 and b = -1 into the slope-intercept formula:

`\Large\boxed{\boxed{y=-x-1}}`