For arbitrarily small positive U, the ground state might not remain bound, and the minimal required value
 for a bound state would be E/6, where E is the energy of the ground state for
for a bound state would be E/6, where E is the energy of the ground state for
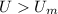 . Obtaining the energy E for small
. Obtaining the energy E for small
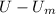 would involve advanced analysis or numerical methods.
would involve advanced analysis or numerical methods.
The ground state for a particle in a spherically symmetric potential can be determined by examining the behavior of the potential at small distances compared to the characteristic length scales involved.
(a) Bound State for Small Energy Parameter U:
For arbitrarily small positive values of U, the ground state might not be a bound state. As U decreases, the potential well becomes shallower, and the binding energy might become insufficient to keep the particle bound.
(b) Minimal Required Value
 for a Bound State:
for a Bound State:
To determine the minimal
 for which the ground state is bound, we analyze when the binding energy matches the depth of the potential well. When the binding energy is equal to the depth of the potential well
for which the ground state is bound, we analyze when the binding energy matches the depth of the potential well. When the binding energy is equal to the depth of the potential well
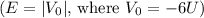 , the particle remains bound.
, the particle remains bound.
Therefore, for the ground state to be bound at
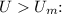
![\[ E = |V_0| = 6U \]](https://img.qammunity.org/2024/formulas/physics/college/pcuc23ghvindaxx0mot51rttf4gtknausn.png)
![\[ E = 6U_m \]](https://img.qammunity.org/2024/formulas/physics/college/3tdt0xcck7psj0ei2il56zbs12t3ko4wb6.png)
The minimal required value
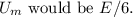
(c) Energy E of the Bound Ground State for Small
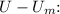
To approximate the energy E of the bound ground state for very small values of
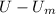 , you can consider using perturbation theory or expansion methods to derive an approximate expression for the energy in terms of
, you can consider using perturbation theory or expansion methods to derive an approximate expression for the energy in terms of
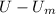 . However, this might require solving the Schrödinger equation in the presence of the S-function potential and performing calculations involving the small parameter
. However, this might require solving the Schrödinger equation in the presence of the S-function potential and performing calculations involving the small parameter
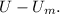
The energy E in the limit of very small values of
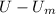 would likely be a function depending on the difference
would likely be a function depending on the difference
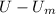 and the parameters of the potential, possibly requiring numerical or advanced analytical techniques to obtain precise values.
and the parameters of the potential, possibly requiring numerical or advanced analytical techniques to obtain precise values.