Answer:
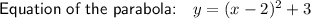
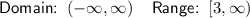

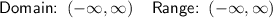
Explanation:
Graph 1 (Parabola)
The given graph shows an upward-opening parabola with its vertex at (2, 3) and a y-intercept at (0, 7).
To write an equation for this parabola, we can use the vertex form of a quadratic equation:

Since the vertex (h, k) is at (2, 3), we can substitute h = 2 and k = 3 into the formula:
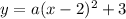
To find the value of a, substitute the y-intercept (0, 7) into the equation:
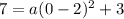
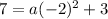
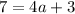
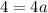

Therefore, the equation of the graphed parabola is:
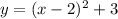
To express the equation in standard form, expand the brackets:
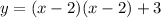
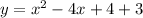
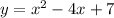
The domain of a function is the set of all possible input values (x-values) for which the function is defined. Since the domain of a quadratic equation is unrestricted, the domain of the graphed parabola is (-∞, ∞).
The range of a function is the set of all possible output values (y-values) for which the function is defined. Since the vertex is the minimum value of the parabola, the range is restricted to all real numbers greater than or equal to the y-value of the vertex. Therefore, the range of the graphed parabola is [3, ∞).

Graph 2 (Cubic function)
The given graph shows a cubic function with an inflection point at (2, 3) and a y-intercept at (0, -5).
To write an equation for this cubic function, we can begin with the parent function, y = x³.
The inflection point of the parent function is located at the origin (0, 0). Therefore, the graphed function can be obtained by translating the parent function 2 units to the right and 3 units up. When we translate a function "n" units to the right, we subtract "n" from the x-variable. When we translate a function "n" units up, we add "n" to the function. Therefore, the equation for the translated function is:
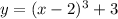
At this stage, we introduce the possibility of a leading coefficient, denoted as "a" which may affect the function's scale. Therefore, we represent the equation as:
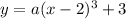
To find the value of a, substitute the y-intercept (0, -5) into the equation:
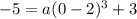
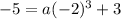
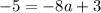
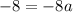

Therefore, the equation of the graphed cubic function is:
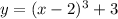
To express the equation in standard form, expand the brackets:

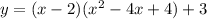
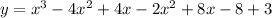
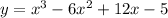
The domain of a function is the set of all possible input values (x-values) for which the function is defined. Since the domain of a cubic function is unrestricted, the domain of the graphed function is (-∞, ∞).
The range of a function is the set of all possible output values (y-values) for which the function is defined. Since the range of a cubic function is unrestricted, the range of the graphed function is (-∞, ∞).