Question

a balloon is ascending at 3.0 m/s at a height of 20.0 m above ground when a package is released. the time taken, in the absence of air resistance, for the package to reach the ground is:

Answer 1

Approximately
`2.35\; {\rm s}`, assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.

Step-by-step explanation:

Under the assumptions, the package would start with an initial upward velocity of
`u = 3.0\; {\rm m\cdot s^(-1)}` and accelerate downward at a constant
`a = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}` (negative because acceleration points downward.)

Right before landing, the package would be
`20.0\; {\rm m}` below where it was released. Hence, the displacement of the package at that moment would be
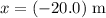`x = (-20.0)\; {\rm m}` (negative since this position is below the initial position.)

The duration of the motion can be found in the following steps:

• Apply the SUVAT equation
  `v^(2) - u^(2) = 2\, a\, x` to find velocity
  `v` right before landing.
• Divide the change in velocity
  `(v - u)` by acceleration to find the duration of the motion.

Rearrange the SUVAT equation
`v^(2) - u^(2) = 2\, a\, x` to find
`v`, the velocity of the package right before reaching the ground. Notice that because the package would be travelling downward, the value of
`v\!` should be negative.

`\begin{aligned} v &= -\sqrt{u^(2) + 2\, a\, x} \\ &= -\sqrt{(3.0)^(2) + 2\, (-9.81)\, (-20.0)}\; {\rm m} \\ &\approx (-20.035)\; {\rm m}\end{aligned}`.

Subtract the initial velocity from the new value to find the change in velocity. Divide this change in velocity by acceleration (rate of change in velocity) to find the duration of the motion:

`\begin{aligned}t &= (v - u)/(a) \\ &\approx ((-20.035) - (3.0))/((-9.81))\; {\rm s} \\ &\approx 2.35\; {\rm s}\end{aligned}`.