Question

Georgina rewrites the expression x² + px + q by completing the square.

He correctly obtains (x - 5)² + 31
Work out the values of p and q.

Answer 1

p= -10, q=56

explanation:

(x - 5)² + 31

If we were to expand this equation, we get

x²-10x+56

therefore x²+px+q, p=-10, q=56

Answer 2

Hello!

Answer:

`\large \boxed{\sf p = -10,~~q =56}`

Explanation:

▪ We want to find the values of p and q.

▪ Let's simplify the following expression:

`\sf (x - 5)^2 + 31`

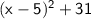
▪ Let's simplify (x - 5)²:

▪ We know that
`\sf(a-b)^2` is equal to
`\sf a^2 - 2ab+b^2`.

In our expression:

`\sf a = x\\b = 5`

▪ So:

`\sf (x - 5)^2 \\\\= x^2-2 * x * 5+5^2\\\\= x^2 - 10x+25`

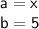
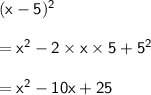
▪ So the expression (x - 5)² + 31 is equal to:

`\sf x^2 - 10x+25+31\\\\= x^2 - 10x+56`

▪ So in the expression (x - 5)² + 31:

`\boxed{\sf p = -10,~~q =56}`

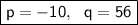
Conclusion:

p = -10

q = 56