Question

A construction company has adjoined a 500 ft2 rectangular enclosure to its office building. Three sides of the enclosure are fenced in. The side of the building adjacent to the enclosure is 50 ft long and a portion of this side is used as the fourth side of the enclosure. Let x and y be the dimensions of the enclosure, where x is measured parallel to the building, and let L be the length of fencing required for those dimensions.

(a) Find a formula for L in terms of x and y
b) Find a formula that expresses L as a function of x alone
c) what is the domain of the function in part b?

Answer 1

The length of fencing required for those dimensions is:

`(a) \( L = x + 2y + 50 \)`

`(b) \( L = x + 2(500/x) + 50 \)`

`(c) \( x > 0 \)`

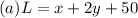
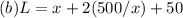
Step-by-step explanation:

In part (a), we find the formula for the length of fencing,
`\( L \),` in terms of the dimensions
`\( x \) and \( y \).` The length of the building (50 ft) and the two sides parallel to
`\( x \) and \( y \)` are included.

In part (b), we express
`\( L \) as a function of \( x \) alone by substituting \( y = (500)/(x) \)`since the total area
`\( xy = 500 \) ft². This simplifies the formula to \( L = x + 2\left((500)/(x)\right) + 50 \).`

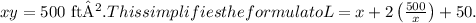
In part (c), we consider the domain of the function in part (b). Since x represents a length, it must be greater than zero. Therefore, the domain is
`\( x > 0 \).`