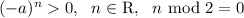Question

What is the limit of the function? f(x)=4x11−3x8+2x−11 Select True or False for each statement. Limit statement True False limx→−∞f(x)=∞ True – limit as x rightwards arrow negative infinity of f left parenthesis x right parenthesis equals infinity False – limit as x rightwards arrow negative infinity of f left parenthesis x right parenthesis equals infinity limx→∞f(x)=−∞ True – limit as x rightwards arrow infinity of f left parenthesis x right parenthesis equals negative infinity False – limit as x rightwards arrow infinity of f left parenthesis x right parenthesis equals negative infinity

Answer 1

`\displaystyle \lim_(x\to\infty)f(x) = \infty, \ \text{DNE}`

`\displaystyle\lim_(x\to-\infty)f(x)= -\infty, \ \ \text{DNE}`

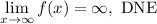
Explanation:

We can find the limit as x approaches infinity for the function:

`\displaystyle f(x)=4x^(11)-3x^8+2x-11`

by examining what happens to each term:

`\displaystyle \lim_(x\to\infty)\!\left(4x^(11)-3x^8+2x-11\right)`

• 
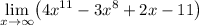
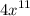  `\displaystyle 4x^{11` goes to infinity because
  `a(\infty)^n = \infty, \ \ a > 0, \ \ n > 0`
• 
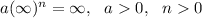
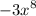  `\displaystyle -3x^8` goes to negative infinity
• 
  `2x` goes to infinity
• 
  `11` is irrelevant

So, we can evaluate the limit as:

`\displaystyle \lim_(x\to\infty)f(x) = \infty - \infty + \infty`

↓ canceling the infinities ...
`a - a = 0`

`\boxed{\displaystyle \lim_(x\to\infty)f(x) = \infty, \ \text{DNE}}`

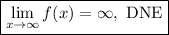
We have to add "DNE" ("Does Not Exist") to the end of our answer because infinity is not a number; therefore it will never be reached.

_____

We can also use the same method to solve for the limit of the function as x approaches negative infinity:

`\displaystyle \lim_(x\to-\infty)\!\left(4x^(11)-3x^8+2x-11\right)`

`= -\infty - \infty -\infty`

`\boxed{\lim_(x\to-\infty)f(x)= -\infty, \ \ \text{DNE}}`

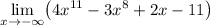
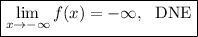
Notice that for the term
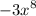`\displaystyle -3x^8`, the
`x`-factor is positive because it is raised to an even power:

`(-a)^n > 0, \ \ n \in \text{R}, \ \ n \!\!\mod 2=0`