Question

Get the roots of the given quadratic equation. After that, get the sum and product of the roots.​

Answer 1

Hi,

Explanation:

P(x)=2x²-3x-20

P(4)=2*4²-3*4-20=32-12-20=0

Factorisation by grouping terms

`2x^2-3x-20=2x^2-8x+5x-20=2x(x-4)+5(x-4)=(x-4)(2x+5)\\`

Roots are 4 and -5/2

In the equation ax²+bx+c=0,

sum of roots is -b/a here -(-3)/2=3/2

Product of roots is c/a here (-20)/2=-10

Answer 2

Roots: x = 4, x = -2.5

Sum of the roots: 1.5

Product of the roots: -10

Explanation:

To find the roots of a quadratic equation in the form ax² - bx - c = 0, we can use the quadratic formula.

`\boxed{\begin{array}{l}\underline{\sf Quadratic\;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\textsf{when} \;ax^2+bx+c=0 \\\end{array}}`

In the case of 2x² - 3x - 20, the values of a, b and c are:

• a = 2
• b = -3
• c = -20

Substitute these values into the quadratic formula:

`x=(-(-3) \pm √((-3)^2-4(2)(-20)))/(2(2))`

`x=(3 \pm √(9+160))/(4)`

`x=(3 \pm √(169))/(4)`

`x=(3 \pm √(13^2))/(4)`

`x=(3 \pm 13)/(4)`

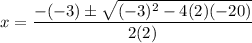
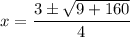
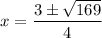
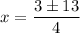
Now, we have two possible solutions for x:

`x_1=(3 + 13)/(4)=(16)/(4)=4`

`x_2=(3 - 13)/(4)=(-10)/(4)=-(5)/(2)=-2.5`

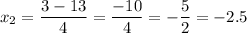
So, the roots of the given quadratic equation 2x² - 3x - 20 are:

• x₁ = 4
• x₂ = -2.5

To find the sum of the roots, simply add x₁ and x₂​:

`\textsf{Sum:}\quad x_1+x_2=4+\left(-2.5\right)=1.5`

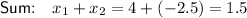
To find the product of the roots, simply multiply x₁ and x₂​:

`\textsf{Product:}\quad x_1\cdot x_2=4\cdot \left(-2.5\right)=-10`

So, the sum of the roots is 1.5, and the product of the roots is -10.