To find the equation of the line passing through the points
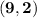 and
and
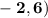 , we first need to calculate the slope
, we first need to calculate the slope
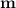 using the formula:
using the formula:
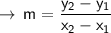
where
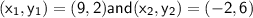 .
.
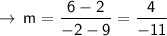
Now that we have the slope
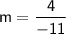 , we can use the point-slope form of the equation of a line:
, we can use the point-slope form of the equation of a line:
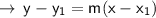
Substituting
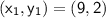 and
and
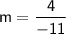 into the equation, we get:
into the equation, we get:
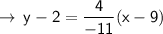
To simplify this equation, first, distribute
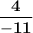 into
into
 :
:
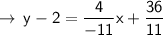
Next, bring
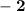 to the right-hand side by adding
to the right-hand side by adding
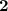 to both sides of the equation:
to both sides of the equation:
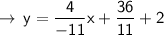
Now, simplify the equation further:
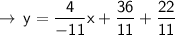

Therefore, the equation of the line passing through
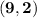 and
and
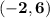 in simplest fractional form is:
in simplest fractional form is:


♥️
