Question

(Multiplying and Dividing with Scientific Notation MC)

1.365 x 10¹8
————————
9.1x108
Divide



A 0.15 x 1010
B 1.5 x 10⁹
C 0.15 x 1026
D 1.5 x 101
Write the final answer in scientific notation.

Answer 1

Ok

Explanation:

To divide the given numbers in scientific notation, you subtract the exponent in the denominator from the exponent in the numerator, and divide the coefficients.

For this problem:

\[

\frac{1.365 \times 10^{18}}{9.1 \times 10^{8}}

\]

First, divide the coefficients:

\[

\frac{1.365}{9.1} = 0.15

\]

Next, subtract the exponent in the denominator from the exponent in the numerator:

\[

18 - 8 = 10

\]

Therefore, the answer in scientific notation is \(0.15 \times 10^{10}\), which is option D.

Answer 2

B. 1.5×10⁹

Explanation:

You want the quotient (1.365×10¹⁸)/(9.1×10⁸) expressed in scientific notation.

Quotient

We can consider the exponential factors separately from the coefficient factors. For a result with a coefficient in the range of 1–10, it is convenient to adjust the numbers we start with.

We know that 1.365/9.1 will be a value less than 1. If we adjust the denominator to 0.91, then the result will be in the range 1–10, as we want.

This suggests we rewrite the denominator as ...

9.1×10⁸ = 0.91×10⁹

Now, our division problem is ...

`(1.365*10^(18))/(9.1*10^8)=(1.365*10^(18))/(0.91*10^9)=(1.365)/(0.91)*10^(18-9)=\boxed{1.5*10^9}\qquad\text{choice B}`

__

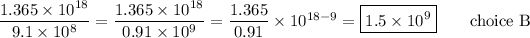
Additional comment

For the powers of 10, the usual exponent rules apply:

(a^b)/(a^c) = a^(b-c)

As the attachment shows, your calculator can do this, too.

<95141404393>