Maximize- p=3x+2y Please explain

Question

asked Nov 13, 2024 66.6k views

1 Answer

Amanni · Answer 1 · 2024-11-17T14:19:09+0000

Answer:

no maximum value

Explanation:

In order to maximize the value of p = 3x + 2y, we need to find the values of x and y that satisfy the following two conditions:

The constraints on x and y can be any set of inequalities that define the feasible region.

For example, the constraints could be:

x ≥ 0

y ≥ 0

To find the values of x and y that maximize p = 3x + 2y and satisfy the constraints, we can use the following steps:

First, find the partial derivatives of p = 3x + 2y with respect to x and y.

The partial derivatives of p = 3x + 2y with respect to x and y are:

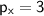
$\sf p_x = 3$

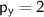
$\sf p_y = 2$

Secondly Set the partial derivatives equal to zero and solve the system of equations.

Setting the partial derivatives equal to zero and solving the system of equations gives us:

3 = 0

2 = 0

Substitute the solutions for x and y into the objective function to find the maximum value of p.

This system of equations has no solutions, which means that there is no maximum value of p = 3x + 2y.

Note:

The objective function is unbounded, meaning that it can be made arbitrarily large.

One way to achieve this is to set x to a very large number and set y to zero.

This will give us a value of p that is equal to 3x.