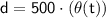Question

A rotating light on top of a lighthouse sends out

rays of light in opposite directions. As the beacon
rotates, the ray at an angle 8 makes a spot of light
that moves along the shore. The lighthouse is
located 500 m from the shoreline and makes
one complete rotation every 2 min.
Determine the equation that expresses the
distance, d, in metres, as a function
of time, t, in minutes.

Answer 1

`\sf d = 500 \cdot (\theta(t))`

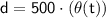
Explanation:

The equation can be derived using the following trigonometric identity:

That is:

`\sf tan(\theta) =( opposite )/( adjacent)`

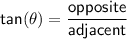
In this case, the opposite side is the distance from the lighthouse to the shoreline and the adjacent side is the distance from the lighthouse to the spot of light on the shoreline (500m)

The angle is equal to the angle of the light beam.

It is changeable according to the time. so,

`\sf \theta \textsf{ will be } \theta t`

Substituting these values into the trigonometric identity gives us the following equation:

`\sf tan(\theta t) = (d)/(500)`

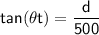
Solving for d gives us the following equation:

`\sf d = 500 \cdot (\theta(t))`

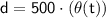
Therefore, the equation to express the distance, d, in metres, as a function of time, t, in minutes is:

`\sf d = 500 \cdot (\theta(t))`