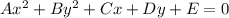Question

Find an equation of the circle, in standard form, whose diameter has endpoints (-1,-6)(3,-2)

After you find the equation in standard form also write the equation of the circle in general form.

Answer 1

Answers:

Standard form:
`(x-1)^2+(y+4)^2 = 8`

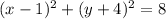
General form:
`x^2+y^2-2x+8y+9 = 0`
=======================================

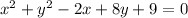
Step-by-step explanation

The endpoints of the diameter are (-1,-6) and (3,-2)

Use the midpoint formula to determine the center of the circle is (1,-4)

Then use the distance formula to calculate how far it is from the center to either endpoint. I'll use the distance formula on (-1,-6) and (1,-4)

`(x_1,y_1) = (-1,-6) \text{ and } (x_2, y_2) = (1,-4)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((-1-1)^2 + (-6-(-4))^2)\\\\d = √((-1-1)^2 + (-6+4)^2)\\\\d = √((-2)^2 + (-2)^2)\\\\d = √(4 + 4)\\\\d = √(8)\\\\`

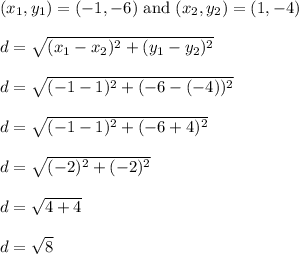
The radius of the circle is exactly
`√(8)` units long.

-------------

We have determined the following so far:

• (h,k) = (1,-4) = center
• r =
  `√(8)` = radius

Plug those values into the standard template
`(x-h)^2+(y-k)^2 = r^2`

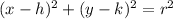
to get
`(x-1)^2+(y-(-4))^2 = (√(8))^2`

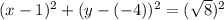
That simplifies to
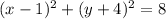`(x-1)^2+(y+4)^2 = 8` which is the equation of the circle in standard form.

-------------

Let's expand that out to get the general form.

`(x-1)^2+(y+4)^2 = 8\\\\x^2-2x+1+y^2+8y+16 = 8\\\\x^2-2x+1+y^2+8y+16-8 = 0\\\\x^2-2x+y^2+8y+9 = 0\\\\x^2+y^2-2x+8y+9 = 0\\\\`

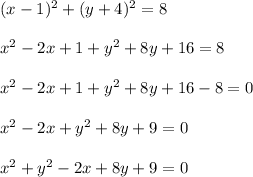
The general form template is
`Ax^2+By^2+Cx+Dy+E = 0`