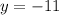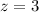Question

2x-y+4z=33

x+2y-3z=-26
-5x-3y+5z=23
Solve the following system of equations using either Gaussian elimination or a matrix. Write your answer as a point and explain how you would check your work:

Answer 1

• x = 5
• y = -11
• z = 3

Task :

To solve the given system of equations using the Gaussian Elimination .

Solution :

• In order to find the values of the variables using gaussian elimination method, we firstly will write augmented matrix of the system of the equations given and then perform row operations to turn the matrix into row-echelon form and further back substitution to find the value of each variable.

The augmented matrix of the system :

[ 2 -1 4 | 33 ]

[1 2 -3 | -26 ]

[-5 -3 5 | 23 ]

Now,

The purpose of performing row operations is to eliminate the coefficient of x in 2nd and the 3rd row.

• Firstly, we'll eliminate the coefficient of x of the 2nd row by multiplying the 2nd row by 2 and subtracting the first row from it and in order to eliminate the coefficient of x from the 3rd row, we'll add 5 times the first row to twice the 3rd row.

In short,

• R2 = 2R2 - R1
• R3 = 5R1 +2R3

The Resultant matrix would be :

[2 -1 4 | 33]

[0 5 -10 | -85]

[0 - 11 30 | 211]

Now,

• We'll eliminate the coefficient of y in the 3rd row making it zero in order to isolate z and find it's value.

The coefficient of y in the 3rd row can be eliminated by adding 11 times the 2nd row to 5 times the 3rd.

In short,

• R3 = 11R2 + 5R3

We'll get,

[2 -1 4 | 33]

[0 5 -10 | -85]

[0 0 40 | 120]

From the resultant 3rd row, we can solve for z :

• 40z = 120
• z = 120/40
• z = 3

Substituting z = 3 in the 2nd row, we get :

• 5y -10*3 = -85
• 5y -30 = -85
• 5y = -85-30
• 5y = -55
• y = -55/5
• y = -11

Substituting y = -11 and z = 3 in the 1st row :

• 2x -(-11) +4*3 = 33
• 2x +11 + 12 = 33
• 2x + 23 = 33
• 2x = 33-23
• 2x = 10
• x = 10/2
• x = 5

Hence,

• x = 5 , y = -11 and z = 3

Verification :

• In order to check whether the resulting values are correct or not, we'll plug in the values in each equation and check whether the values are true or not for each equation.

#1

2x-y+4z=33

2*5 -(-11)+4*3 = 33

10+11 + 12 = 33

33 = 33

LHS = RHS,hence true ✓

#2

x+2y-3z=-26

5 +2*(-11) -3*3 = -26

5 -22 -9 = -26

5 -31 = -26

-26 = -26

LHS = RHS ,hence true ✓

#3

-5x-3y+5z=23

-5*5 - 3*(-11) +5*3 = 23

-25 +33 +15 = 23

23 = 23

LHS = RHS ,hence true

Hence, verified ✓

`\:`

Answer 2

x = 5

y = -11

z = 3

Explanation:

To solve the system of equations using Gaussian elimination, first write the system in augmented matrix form and then perform row operations to simplify it.

The system of equations is:

`\begin{cases}2x - y + 4z = 33\\x + 2y - 3z = -26\\-5x - 3y + 5z = 23\end{cases}`

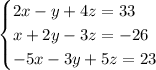
Create an augmented matrix [A|B] where A represents the coefficients of the variables (x, y, z), and B represents the constants on the right-hand side of each equation:

`[A|B] = \left[\begin{array}rrr2 & -1 & 4 & 33 \\1 & 2 & -3 & -26 \\-5 & -3 & 5 & 23 \\\end{array}\right]`

Now use row operations to simplify the augmented matrix into its reduced echelon form where:

• The leading entry (the leftmost non-zero entry) in any non-zero row is 1.
• The leading entry of each non-zero row after the first row must be to the right of the leading entry of the previous row.
• All entries in the column below a leading 1 are zero.

Switch the first row (R₁) and the second row (R₂):

`\left[\begin{array}r2 & -1 & 4 & 33 \\1 & 2 & -3 & -26 \\-5 & -3 & 5 & 23 \\\end{array}\right]R_1\leftrightarrow R_2 \left[\begin{array}rrr1 & 2 & -3 & -26 \\2 & -1 & 4 & 33 \\-5 & -3 & 5 & 23 \\\end{array}\right]`

Subtract 2 times the first row (R₁) from the second row (R₂):

Add 5 times the first row (R₁) to the third row (R₃):

Multiply the second row (R₂) by -1/5:

`\left[\begin{array}r1 & 2 & -3 & -26 \\0 & -5 & 10 & 85 \\0 & 7 & -10 & -107 \\\end{array}\right]-(1)/(5)R_2\rightarrow R_2\left[\begin{array}rrr1 & 2 & -3 & -26 \\0 &1 & -2 & -17 \\0 & 7 & -10 & -107 \\\end{array}\right]`

Subtract 7 times the second row (R₂) from the third row (R₃):

`\left[\begin{array}r1 & 2 & -3 & -26 \\0 &1 & -2 & -17 \\0 & 7 & -10 & -107 \\\end{array}\right]R_3-7R_2\rightarrow R_3\left[\begin{array}r1 & 2 & -3 & -26 \\0 &1 & -2 & -17 \\0 & 0 & 4 & 12 \\\end{array}\right]`

Finally, multiply the third row (R₃) by 1/4:

`\left[\begin{array}rrr1 & 2 & -3 & -26 \\0 &1 & -2 & -17 \\0 & 0 & 4 & 12 \\\end{array}\right](1)/(4)R_3\rightarrow R_3\left[\begin{array}rrr1 & 2 & -3 & -26 \\0 &1 & -2 & -17 \\0 & 0 & 1 & 3 \\\end{array}\right]`

Now this is in reduced echelon form, we can deduce the value z from R₃:

`z=3`

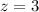
Substitute the value of z into R₂ and find the value of y:

`\begin{aligned}y-2z&=-17\\y-2(3)&=-17\\y-6&=-17\\y&=-11\end{aligned}`

Finally, substitute the values of y and z into R₁ to find the value of x:

`\begin{aligned}x+2y-3z&=-26\\x+2(-11)-3(3)&=-26\\x-22-9&=-26\\x-31&=-26\\x&=5\end{aligned}`

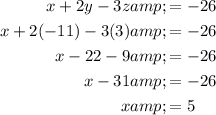
So, the solution to the system of equations is:

• x = 5
• y = -11
• z = 3

`\hrulefill`

Additional Notes

Another common definition of reduced echelon form requires that all entries in the column above and below a leading 1 are zero.

If this is the definition you need to use, continue simplifying with the following operations:

Subtract 2 times the second row (R₂) from the first row (R₁):

`\left[\begin{array}r1 & 2 & -3 & -26 \\0 &1 & -2 & -17 \\0 & 0 & 1 & 3 \\\end{array}\right]R_1-2R_2\rightarrow R_1\left[\begin{array}rrr1 & 0 & 1 & 8 \\0 &1 & -2 & -17 \\0 & 0 & 1 & 3 \\\end{array}\right]`

Add 2 times the third row (R₃) to the second row (R₂):

`\left[\begin{array}r1 & 0 & 1 & 8 \\0 &1 & -2 & -17 \\0 & 0 & 1 & 3 \\\end{array}\right]R_2+2R_3\rightarrow R_2\left[\begin{array}r1 & 0 & 1 & 8 \\0 &1 & 0 & -11 \\0 & 0 & 1 & 3 \\\end{array}\right]`

Subtract the third row (R₃) from the first row (R₁):

`\left[\begin{array}rrr1 & 0 & 1 & 8 \\0 &1 & 0 & -11 \\0 & 0 & 1 & 3 \\\end{array}\right]R_1-R_3\rightarrow R_1\left[\begin{array}r1 & 0 & 0& 5 \\0 &1 & 0 & -11 \\0 & 0 & 1 & 3 \\\end{array}\right]`

We can now deduce the value of x from R₁, the value of y from R₂ and the value of z from R₃:

`x=5`

`y = -11`

`z = 3`