Question

3. Walter’s is five years older than Carla. Their combined age is 78 years old. How old are Walter and Carla? a) Write an equation that represents the situation. Explain any variable used. a. Please be aware that as an Applied Question on the Applied Part of your Unit Test that the goal of this question is to assess your ability to create and solve equations from a situation. b) Solve the equation from Part (a). Show your work. State your solution as a complete sentence.

Answer 1

Explanation:

let Carla's age be x

Walter's age is x + 5

Their combined age is 78

x + x + 5 = 78

2x = 78 - 5

2x = 73

x = 36.5

Carla's age is 36.5 or 36 and 1/2 years old

Walter's age is 41.5 or 41 and 1/2 years old

Answer 2

Part A:

Equation that represent situations are:

`\sf w = c + 5`

`\sf w + c = 78`

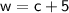
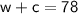
Variable used:

Age of Walter = w

Age of Carla = c

Part B

Age of Walter = 41 years and 6 months old

Age of Carla = 36 years and 6 months old

Explanation:

Part a):

Let Walter's age be w and Carla's age be c.

The problem states that Walter is five years older than Carla, so we can write the following equation:

`\sf w = c + 5`

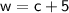
This equation tells us that Walter's age is equal to Carla's age plus 5 years.

The problem also states that their combined age is 78 years old. We can write this information as the following equation:

`\sf w + c = 78`

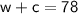
This equation tells us that the sum of Walter's age and Carla's age is equal to 78 years.

b)

To solve for w and c, we can use the following steps:

Substitute the first equation into the second equation. This gives us:

`\sf (c + 5) + c = 78`

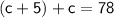
Combine like terms:

`\sf 2c + 5 = 78`

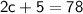
Subtract 5 from both sides:

`\sf 2c + 5 - 5 = 78 - 5`

`\sf 2c = 73`

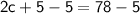
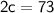
Divide both sides by 2:

`\sf (2c)/(2) = (73)/(2)`

`\sf c = 36.5`

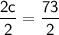
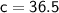
Now that we know c, we can substitute it back into the first equation to solve for w.

`\sf w = 36.5 + 5`

`\sf w = 41.5`

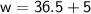
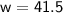
Therefore, Walter is 41.5 years old or 41 years and 6 months old and Carla is 36.5 years old or 36 years and 6 months old.