Question

Verify 1/sin(x)cos(x) - cot(x) = tan(x) with steps. Please answer quickly, thank you :)

Answer 1

True

Explanation:

We can verify the trigonometric identity:

`(1)/(\sin(x)\cos(x)) - \cot(x) = \tan(x)`

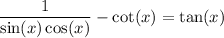
by finding a common denominator for the terms on the left side, then canceling factors in the numerator and denominator until we get the definition for tangent, which is:

`\tan(x) = (\sin(x))/(\cos(x))`

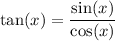
First, we can expand the term cot(x) with its definition:

`(1)/(\sin(x)\cos(x)) - (\cos(x))/(\sin(x)) = \tan(x)`

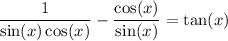
Next, to get a common denominator, we can multiply the cot(x) term by
`(\cos(x))/(\cos(x))`:

`(1)/(\sin(x)\cos(x)) - \left((\cos(x))/(\sin(x))\right) \!\left((\cos(x))/(\cos(x))\right) = \tan(x)`

`(1)/(\sin(x)\cos(x)) - ((\cos(x))^2)/(\sin(x)\cos(x)) = \tan(x)`

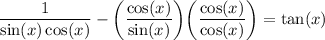
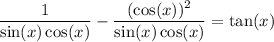
Then, we can combine the fractions because they have a common denominator of sin(x) cos(x):

`(1 - (\cos(x))^2)/(\sin(x)\cos(x)) = \tan(x)`

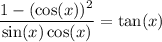
From here, we have to manipulate the Pythagorean Identity:

`(\sin(x))^2+(\cos(x))^2=1`

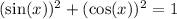
so that we have 1 - (cos(x))² on one side:

`(\sin(x))^2=1-(\cos(x))^2`

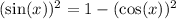
Now, we can substitute this identity into the numerator of the left side of the identity we are verifying:

`((\sin(x))^2)/(\sin(x)\cos(x)) = \tan(x)`

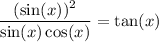
We can see that sin(x) is a common factor in the numerator and denominator, so we can cancel it from both:

`(\sin(x))/(\cos(x)) = \tan(x)`

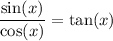
Finally, we can see that the identity is true because it yields the definition of tangent.