Answer:
Linear relationship is: P = -0.004n +90
Explanation:
We can use the following linear equation to model the relationship between the number of shirts sold and the price charged per shirt:
P = mn + b
where:
- P is the price charged per shirt
- n is the number of shirts sold
- m is the slope of the line
- b is the y-intercept
We can use the two data points given in the problem to solve for the slope and y-intercept of the line.
(3000, 78)
(7000, 62)
Substituting the first data point into the equation gives us:
78 = m × 3000 + b
78 = 3000m + b
Substituting the second data point into the equation gives us:
62 = m × 7000 + b
62 = 7000m + b
Subtracting the second equation from the first equation gives us:
62 - (78) = 7000m + b - ( 3000m +b)
Open the bracket:
62 - 78 = 7000m + b - 3000m - b
Simplify like terms:
- 16 = 4000m
Divide both sides by 4000.
we get
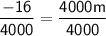
m = -0.004
Substituting this value of m into either of the original equations and solving for b gives us:
78 = - 0.004 × 3000 + b
78 = - 12 + b
isolate b, we get
b = 78 + 12
b = 90
Therefore, the linear equation that models the relationship between the number of shirts sold and the price charged per shirt is:
P = -0.004n +90
We can use this equation to predict the price that the clothing business can charge for any number of shirts.
For example, if the clothing business wants to sell 5000 shirts, we can use the equation to predict the price as follows:
P = -0.004 × 5000 + 90 = 70
Therefore, the clothing business can charge $70 per shirt if it wants to sell 5000 shirts.