Question

Please help, I'm crying over here I cant get the answers 100 points

Answer 1

Both are 6

Choose two y values and the corresponding x values.

Plug them into this equation y2-y1 over x2-x1

Also since they are both the same they are parallel

Answer 2

`\sf \textsf{Slope of line 1 }= 6`

`\sf \textsf{Slope of line 2 }= 6`

and Parallel

Explanation:

The slope of a line is a measure of its steepness. It is calculated as the change in the y-coordinate divided by the change in the x-coordinate between two points on the line.

The slope of a line is represented by the letter m.

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

where:

• y2 and y1 are the y-coordinates of the two points
• x2 and x1 are the x-coordinates of the two points

For line 1:

Let's take two points:

(-10, -61) and (30, 179)

Substituting these value of points, we get:

`\sf m = (179 - (-61))/(30 - (-10))`

`\sf m = ( 240)/(40)`

`\sf m =6`

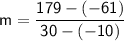
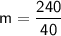
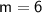
Therefore,

`\sf \textsf{Slope of line 1 }= 6`

Similarly:

For line 2:

Let's take two points:

(-5, -39) and (40, 231)

Substituting these value of points, we get:

`\sf m = (231 - (-39))/(40 - (-5))`

`\sf m = ( 270 )/(45)`

`\sf m = 6`

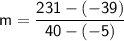
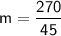
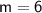
Therefore,

`\sf \textsf{Slope of line 2 }= 6`

Note:

In Parallel lines: Slopes are equal.

In Perpendicular lines: Slopes are negative reciprocals of each other.

In this case:

Slope of line 1 = Slope of line 2.

It fullfill the conditions of parallel lines.

So, they are parallel to each other: