Question

Help me please!!! and thank you

Answer 1

10 + 3π ≈ 19.4

Explanation:

The radius of the quarter circle SBT is 6 units.

As the diagonals (AC and RB) of rectangle ABCR are equal to the radius of SBT, then AC = 6 units.

The formula for the diagonal (d) of a rectangle with width "x" and length "y" is:

`d=√(x^2+y^2)`

Therefore, as the diagonal of rectangle ABCR is 6 units, then:

`6=√(x^2+y^2)`

Given that the length plus the width of ABCR is 8 units, then y + x = 8.

Rearranging the equation to isolate x gives y = 8 - x.

Substitute this into the diagonal equation:

`6=√(x^2+(8-x)^2)`

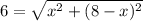
Square both sides of the equation:

`6^2=\left(√(x^2+(8-x)^2)\right)^2`

`36=x^2+(8-x)^2`

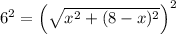
Rearrange:

`36=x^2+64-16x+x^2`

`36=2x^2+64-16x`

`2x^2-16x+28=0`

`2(x^2-8x+14)=0`

`x^2-8x+14=0`

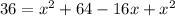
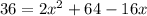
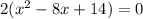
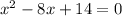
Solve for x using the quadratic formula:

`x=(-(-8)\pm√((-8)^2-4(1)(14)))/(2(1))`

`x=(8\pm√(8))/(2)`

`x=(8\pm2√(2))/(2)`

`x=4\pm √(2)`

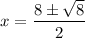
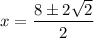
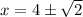
Substitute the values of x into the equation for y:

`y=8-(4\pm √(2))`

`y=4\pm √(2)`

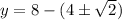
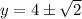
As the width (RC) of rectangle ABCR is smaller than its length (AR), then:

• RC = 4 - √2
• AR = 4 + √2

RT and SR are the radii of the quarter circle, so:

• RT = 6
• SR = 6

To find the lengths of CT and SA, we can subtract RC from RT, and subtract AR from SR:

`\begin{aligned}CT&=RT-RC\\&=6-(4-√(2))\\&=2+√(2)\end{aligned}`

`\begin{aligned}SA&=SR-AR\\&=6-(4+√(2))\\&=2-√(2)\end{aligned}`

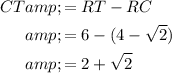
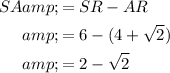
To calculate the length of arc SBT, use the arc length formula:

`\textsf{Arc length}= \pi r\left((\theta)/(180^(\circ))\right)`

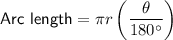
In this case, r = 6 and θ = 90°. Therefore:

`\textsf{Arc $SBT$}&= \pi (6)\left((90^(\circ))/(180^(\circ))\right)=3\pi`

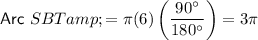
Finally, to calculate the perimeter of the shaded region, sum the lengths of SA, AC, CT and arc SBT:

`\begin{aligned}\textsf{Perimeter}&=SA+AC+CT+\overset{\frown}{SBT}\\&=(2-√(2))+6+(2+√(2))+3\pi\\&=10+3\pi\end{aligned}`

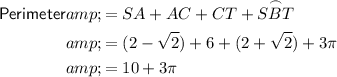
Therefore, the exact perimeter of the shaded region is equal to 10 + 3π units, or approximately 19.4 units (rounded to the nearest tenth).