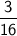Question

Need help with probability distributions.

Find the probability for each situation.

a) On average, 5.5 people immigrate to the us in 1 hour. .Find the probability that this hour, 2 people immigrated to the U.S

b) 18% of U.S. citizens use red.dit. If you randomly chose 12 people, find the probability that 5 of them use red,dit.

c) A cereal maker puts a prize in 1/4 of boxes. Find the probability that you get your first prize on your second box.

Answer 1

a) 0.0618 (3 s.f.)

b) 0.0373 (3 s.f.)

c) 0.1875

Explanation:

Question a)

To find the probability of 2 people immigrating to the U.S. when, on average, 5.5 people immigrate in 1 hour, we can use the Poisson distribution formula:

`\boxed{P(X=x)=(\lambda^xe^(-\lambda))/(x!)}`

where:

• x = 0, 1, 2, 3...
• e is Euler's number (constant).
• λ is the mean of the distribution.

We use the Poisson probability formula because it models events with a known average rate of occurrence in a fixed interval of time or space.

In this case:

• x = 2
• λ = 5.5

Substitute the values into the formula:

`P(X=2)=(5.5^(2)\cdot e^(-5.5))/(2!)`

`P(X=2)=(30.25\cdot e^(-5.5))/(2)`

`P(X=2)=0.0618124180...`

Therefore, the probability that 2 people immigrated to the U.S this hour is 0.0618 (3 s.f.).

`\hrulefill`

Question b)

To find the probability that 5 out of 12 randomly chosen people use a certain website when 18% of U.S. citizens use that website, we can use the binomial probability formula:

`\boxed{\displaystyle P(X = x) = \binom{n}{x} \cdot p^x \cdot (1 - p)^(n - x)}`

where:

• n is the number of trials.
• p is the probability of success.
• x is the number of successful trials.

We use the binomial probability formula as it deals with the probability of a fixed number of successes, in a fixed number of trials, with a known probability of success.

In this case:

• x = 5
• n = 12
• p = 0.18

Substitute the values into the formula:

`\displaystyle P(X = 5) = \binom{12}{5} \cdot 0.18^5 \cdot (1 - 0.18)^(12 - 5)`

`P(X = 5) =(12!)/(5!(12-5)!) \cdot 0.18^5 \cdot 0.82^(7)`

`P(X = 5) =792 \cdot 0.0001889568 \cdot 0.24928547056768`

`P(X = 5) =0.03730651436553...`

Therefore, the probability that 5 out of 12 randomly chosen people use a certain website is 0.0373 (3 s.f.).

`\hrulefill`

Question c)

To find the probability of getting a first prize on the second box of cereal when 1/4 of the boxes contain a prize, we can use the geometric probability formula:

`\boxed{P(X = x) = (1 - p)^(x-1) \cdot p}`

where:

• x is the number of trials until the first success
• p is the probability of a success for one trial.

We use the geometric probability formula because it calculates the probability of achieving a specific success on a repeated trial until success is achieved, with a constant probability of success.

In this case:

• x = 2
• p = 1/4 = 0.25

Substitute the values into the formula:

`P(X = 2) = (1 - 0.25)^(2-1) \cdot 0.25`

`P(X = 2) = (0.75)^(1) \cdot 0.25`

`P(X = 2) = 0.75 \cdot 0.25`

`P(X = 2) = 0.1875`

Therefore, the probability of getting a first prize on the second box of cereal when 1/4 of the boxes contain a prize is 0.1875.

Answer 2

a) 0.062

b) 0.037

c)
`\sf (3)/(16)`

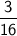
Explanation:

Part a) This situation involves a Poisson distribution because we are dealing with the number of events (people immigrating) in a fixed interval of time (1 hour) where events occur randomly with a known average rate (5.5 people per hour).

The Poisson probability mass function is given by:

`\sf P(X =x) = (e^(-λ ) \cdot λ^x)/( x!)`

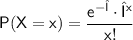
Where:

P(X = x) is the probability of observing events.

e is Euler's number, approximately equal to 2.71828.

λ (lambda) is the average rate of events in the given time interval.

In this case, λ = 5.5 (average number of people immigrating per hour), and we want to find the probability that 2 people immigrated, so x = 2 and simplify.

`\sf \begin{aligned} P(X = 2) & = (e^((-5.5)) \cdot 5.5^2)/(2!) \\\\ &= (0.004086771438 \cdot 30.25)/(2) \\\\ &= ( 0.123624836)/(2) \\\\ &= 0.06181241801 \\\\ &= 0.062 \textsf{ ( in 3 d.p)}\end{aligned}`

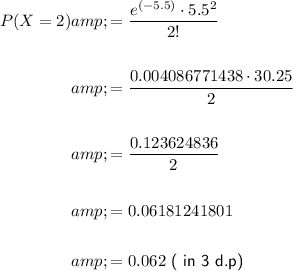
So, the probability that exactly 2 people immigrated to the U.S. in that hour is approximately 0.06.

Part b:

This situation follows a binomial distribution because each person either uses Reddit (success) with a probability of 18% or does not use Reddit (failure) with a probability of 82% in each trial (choosing a person).

The probability mass function for the binomial distribution is given by:

`\sf P(X = x) = C(n, x) \cdot p^x \cdot q^((n - x))`

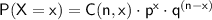
Where:

P(X = x) is the probability of observing x successes.

C(n, x) is the binomial coefficient (number of ways to choose x from n).

p is the probability of success in one trial.

q is the probability of failure in one trial (1 - p).

n is the total number of trials.

In this case, n = 12 (choosing 12 people), p = 0.18 (probability that a person uses Reddit), and we want to find the probability that exactly 5 of them use Reddit, so a = 5.

Probability will be:

`\sf \begin{aligned} P(X = 5) & = C(12, 5) \cdot (0.18^5) \cdot (0.82^7) \\\\ &= 792 \cdot 0.0001889568 \cdot 0.2492854706 \\\\ &= 0.03730651437 \\\\ &= 0.037 \textsf{( in 3 d.p)}\end{aligned}`

So, the probability that exactly 5 out of 12 randomly chosen people use Reddit is approximately 0.037.

Part c:

This situation involves a geometric distribution because we want to find the probability of getting the first prize on the second box. The geometric distribution models the number of trials (in this case, opening boxes) needed until the first success (getting a prize).

The probability mass function for the geometric distribution is given by:

`\sf P(X = x) = (1 - p)^((x - 1)) \cdot p`

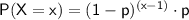
Where:

• P(X = x) is the probability of needing x trials to get the first success.
• p is the probability of success in one trial.
• (1 - p) is the probability of failure in one trial.

In this case, p = 1/4 (probability of getting a prize in one box), and we want to find the probability of getting the first prize on the second box, so x = 2.

So, probability will be:

`\sf \begin{aligned} P(X = 2) & = \left(1 - (1)/(4)\right)^((2 - 1))\cdot (1)/(4) \\\\ &= (3)/(4) \cdot (1)/(4) \\\\ &= ( 3)/(16) \end{aligned}`

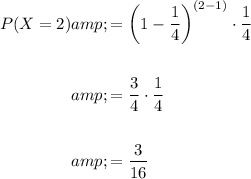
So, the probability of getting your first prize in second box is:

`\sf (3)/(16)`