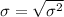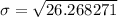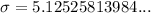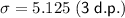Question

Find the mean, variance and standard deviation for the probability distribution given below:

X -2 3 8 11
P(X) 0.551 0.114 0.216 0.119
A. Mean = 2.277
B. Variance =?
C. Standard Deviation =?

Answer 1

A. Mean = 2.277

B. Variance = 26.268 (3 d.p.)

C. Standard Deviation = 5.125 (3 d.p.)

Explanation:

Given probability distribution:

`\begin{array}c\cline{1-5}x&-2&3&8&11\\\cline{1-5}P(x)&0.551&0.114&0.216&0.119\\\cline{1-5}\end{array}`

The mean (μ) of a discrete probability function, often referred to as the expected value E(x), is calculated by multiplying each value of x by its corresponding probability and then summing these products.

`\text{E}(x)=\displaystyle \mu = \sum \left(x\cdot P(x)\right)`

Therefore, the mean of the given probability distribution is:

`\mu = (-2)\cdot 0.551+3 \cdot 0.114+8\cdot 0.216+11\cdot 0.119`

`\mu =-1.102+0.342+1.728+1.309`

`\mu =2.277`

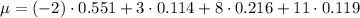
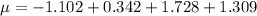
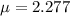
To calculate the variance (σ²), multiply the square each value of x by its corresponding probability, sum these products, then subtract the square of the expected value (μ²).

`\text{Var}(X)=\displaystyle \sigma^2 = \sum(x^2\cdot P(x))-\mu^2`

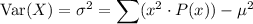
Therefore, the variance of the given probability distribution is:

`\sigma^2= \left[(-2)^2\cdot 0.551+3^2 \cdot 0.114+8^2\cdot 0.216+11^2\cdot 0.119\right]-(2.277)^2`

`\sigma^2= \left[4\cdot 0.551+9 \cdot 0.114+64\cdot 0.216+121\cdot 0.119\right]-5.184729`

`\sigma^2= \left[2.204+1.026+13.824+14.399\right]-5.184729`

`\sigma^2= 31.453-5.184729`

`\sigma^2 = 26.268271`

`\sigma^2 = 26.268\; \sf (3\;d.p.)`

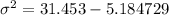
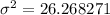
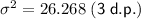
The standard deviation (σ) is the square root of the variance.

Since the variance is 26.268271, the standard deviation is:

`\sigma=√(\sigma^2)`

`\sigma=√(26.268271)`

`\sigma=5.12525813984...`

`\sigma= 5.125\; \sf (3\;d.p.)`