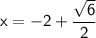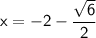What are the solutions to the equation 2x^2 + 4x - 1 = 0

Question

asked Nov 28, 2024 107k views

2 Answers

Kishore Guruswamy · Answer 1 · 2024-12-04T14:37:09+0000

Answer:

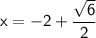
$\sf x = -2 +(√(6))/( 2)$

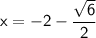
$\sf x = -2 - (√(6))/( 2)$

Explanation:

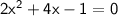
$\sf 2x^2 + 4x - 1 = 0$

This can be found using the quadratic formula, which is:

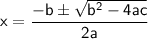
$\sf x = (-b \pm √(b^2 - 4ac))/( 2a)$

where a, b, and c are the coefficients of the quadratic equation.

In this case, a = 2, b = 4, and c = -1.

Substituting these values into the quadratic formula, we get:

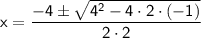
$\sf x = (-4 \pm √(4^2 - 4\cdot 2 \cdot (-1) ))/( 2\cdot 2 )$

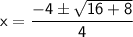
$\sf x = (-4 \pm √(16 +8 ))/( 4 )$

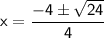
$\sf x = (-4 \pm √(24 ))/( 4 )$

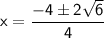
$\sf x = (-4 \pm 2 √(6 ))/( 4 )$

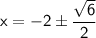
$\sf x = -2 \pm (√(6))/( 2)$

Either

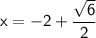
$\sf x = -2 +(√(6))/( 2)$

Or

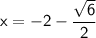
$\sf x = -2 - (√(6))/( 2)$

Therefore, the solutions to the equation are:

$\sf x = -2 +(√(6))/( 2)$

$\sf x = -2 - (√(6))/( 2)$