Question

Determine whether the relationship represents a function: y² + x² = 35

O Function
O Not a function

Answer 1

• Not a function

Solution :

In order to find whether the relationship represents a function or not ,we are required to solve the relationship for a single variable and if it doesn't give a single value of the other variable ,then it isn't a function.

• 
  `y {}^(2) = 35 - x {}^(2)`
• 
  `y = ±\sqrt{35 - x {}^(2) }`

Since ,there are two existing values of x for y ,thus,this relationship doesn't represent a function.

Answer 2

Not a function

Explanation:

A function is a special type of relationship where each input (x-value) is related to exactly one output (y-value).

To determine whether the relationship y² + x² = 35 represents a function, we can solve the equation for y:

`\begin{aligned}y^2 + x^2 &= 35\\\\y^2 + x^2-x^2 &= 35-x^2\\\\y^2&=35-x^2\\\\√(y^2)&=√(35-x^2)\\\\y&=\pm √(35-x^2)\end{aligned}`

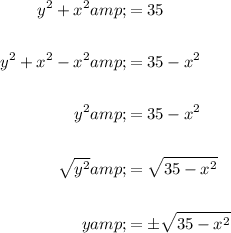
Here, the presence of the ± sign in front of the square root indicates that for some x-values there are two corresponding y-values, which does not conform to the definition of a function.

The vertical line test is a visual method for confirming whether a graph represents a valid function. If a vertical line intersects the graph at more than one point for any x-value in the domain, the graph fails the test and does not represent a valid function.

The graph of the given relationship is a circle centered at the origin (0, 0) with a radius of √(35) units. It fails the vertical line test since a vertical line intersects the graph at more than one point for any x-value in the domain except the leftmost and rightmost x-values.

Therefore, based on both algebraic analysis and the vertical line test, the relation y² + x² = 35 does not represent a function because there are x-values for which there are multiple y-values, and its graph fails the vertical line test.