Question

Which values of x are solutions of the compound inequality? 63x-5-10 x = 3 x = -2 x = 4 x = 5 none of the above​

Answer 1

Answer: x = 3 only

Step-by-step explanation

Let's isolate x.

`6 > 3\text{x}-5 \ge -10\\\\-10 \le 3\text{x}-5 < 6\\\\-10+5 \le 3\text{x}-5+5 < 6+5\\\\5 \le 3\text{x} < 11\\\\5/3 \le 3\text{x}/3 < 11/3\\\\5/3 \le \text{x} < 11/3\\\\1.667 \le \text{x} < 3.667\\\\`

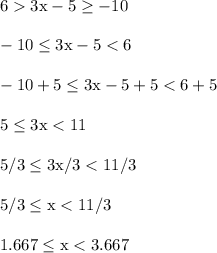
The decimal values are approximate.

If we make x an integer, then the solution set would be {2, 3}

This is because
`1.668 \le 2 < 3.667` and
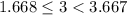`1.668 \le 3 < 3.667` are both true statements.

Let's check x = 2 back in the original inequality.

`6 > 3\text{x}-5 \ge -10\\\\6 > 3*2-5 \ge -10\\\\6 > 6-5 \ge -10\\\\6 > 1 \ge -10\\\\-10 \le 1 < 6 \ \ \ \checkmark`

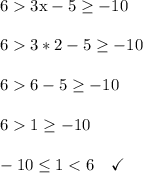
We get a true statement because 1 is indeed between -10 and 6.

If we check x = 3, then,

`6 > 3\text{x}-5 \ge -10\\\\6 > 3*3-5 \ge -10\\\\6 > 9-5 \ge -10\\\\6 > 4 \ge -10\\\\-10 \le 4 < 6 \ \ \ \checkmark`

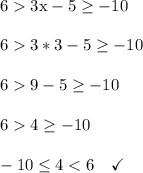
That works as well.

Both solutions x = 2 and x = 3 have been confirmed.

Let's look at an example of a non-solution. Let's try x = 4.

`6 > 3\text{x}-5 \ge -10\\\\6 > 3*4-5 \ge -10\\\\6 > 12-5 \ge -10\\\\6 > 7 \ge -10\\\\-10 \le 7 < 6 \ \ \ \text{ ... false}`

The value 7 is larger than -10, but it's not smaller than 6.

Therefore, 7 is not between -10 and 6. The final inequality being false makes the original inequality false when x = 4. Furthermore, you should find the original inequality is false when x = -7 and x = 5.

In summary, the only answer of the answer choices is x = 3. Unfortunately x = 2 isn't listed. It looks like you selected the correct answer choice.