Question

Jessica deposited $4000 into an account with a 3.6% annual interest rate, compounded quarterly. Assuming that no withdrawals are made, how long will it take for the investment to grow to $6000? Do not round any intermediate computations, and round your answer to the nearest hundredth.

Answer 1

It will take about 11.31 years for Jessica's deposit to grow to $6000.

Explanation:

The formula for compound interest is given by:

`A(t)=P(1+r/n)^(^n^t^)`, where

• A is the amount in the account after t years,
• P is the principal (deposit),
• r is the annual interest rate as a decimal,
• and n is the number of compounding periods.

Identifying our variables:

• Since we want the investment to grow to $6000, it's A.
• Since Jessica deposited $4000 into the account, it's P:
• 3.6% as a decimal is 0.036, so this is r.
• There are 4 compounding periods for money compounded quarterly, as the money is compounded once every three months and there are four of these three month periods w/in a single year (aka 12 months).

Now we can use the following steps to solve for t, the amount of time it will take for Jessica's investment to reach $6000:

Step 1: Plug in 6000 for A, 4000 for P, 0.036 for r, and 4 for n in the compound interest formula. Then simplify:

`6000=4000(1+0.036/4)^(^4^t^)\\\\6000=4000(1.009)^(^4^t^)`

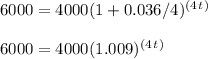
Step 2: Divide both sides by 4000 and simplify:

`(6000=4000(1.009)^(^4^t^))/4000\\\\1.5=1.009^(^4^t^)`

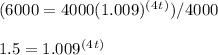
Step 3: Take the log of both sides. Then apply the power rule of logs on the right-hand side to bring 4t down:

`log(1.5)=log(1.009^(^4^t^))\\\\log(1.5)=4t*log(1.009)`

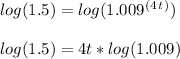
Step 4: Divide both sides by log(1.009):

`(log(1.5)=4t*log(1.009)) / log(1.009)\\\\log(1.5)/log(1.009)=4t`

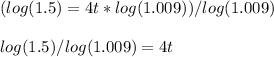
Step 5: Multiply both sides by 1/4 (note, this is the same as dividing by 4). Then write out the numeric answer and round to the nearest hundredth to find the final answer:

`1/4(log(1.5)/log(1.009)=4t)\\\\11.31352712=t\\\\11.31=t`

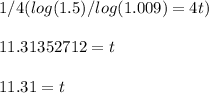
Therefore, it will take about 11.31 years for Jessica's deposit to grow to $6000.