Question

Y-5=x

x + 2y = 22
Which ordered pair (x,y) satisfies the given system of equations?
Choose 1 answer:
(1,6)
(4,9)
(6,8)
(12,17)

Answer 1

(4, 9)

Explanation:

To find the ordered pair (x, y) that satisfies the given system of equations, we can use the method of substitution or elimination. Let's use the elimination method:

Given equations:

`1. \(y - 5 = x\)`

`2. \(x + 2y = 22\)`

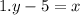
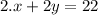
First, let's solve equation 1 for x:

`\[x = y - 5\]`

Now, substitute this expression for x into equation 2:

`\[(y - 5) + 2y = 22\]`

Combine like terms:

`\[3y - 5 = 22\]`

Add 5 to both sides:

`\[3y = 27\]`

Now, divide by 3:

`\[y = 9\]`

Now that we have found the value of y, we can find the value of x using the first equation:

`\[x = y - 5 = 9 - 5 = 4\]`

So, the ordered pair (x, y) that satisfies the system of equations is (4, 9). Therefore, the answer is:

(4, 9)