Question

Solve for y: R (6x-11)° (9y-19)° (4x+23)°​

Answer 1

y = 12

Explanation:

We first need to solve for x

(6x - 11)° and (4x + 23)° are vertically opposite angles and are congruent, so

6x - 11 = 4x + 23 ( subtract 4x from both sides )

6x - 4x - 11 = 4x - 4x + 23 ( simplify both sides )

2x - 11 = 23 ( add 11 to both sides )

2x - 11 + 11 = 23 + 11 ( simplify both sides )

2x = 34 ( divide both sides by 2 )

`(2)/(2)` x =
`(34)/(2)` , that is

x = 17

Then

4x + 23 = 4(17) + 23 = 68 + 23 = 91

(9y - 19)° and 91 are a linear pair and sum to 180°

sum the 2 angles and equate to 180

9y - 19 + 91 = 180 ( simplify left side )

9y + 72 = 180 ( subtract 72 from both sides )

9y + 72 - 72 = 180 - 72 ( simplify both sides )

9y = 108 ( divide both sides by 9 )

`(9)/(9)` y =
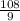`(108)/(9)` , that is

y = 12