Question

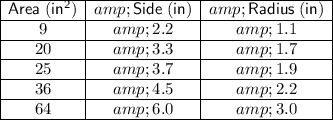
Please help find the answer

Answer 1

`\begin{array}c\cline{1-3}\sf Area\;(in^2)&\sf Side\;(in)&\sf Radius\;(in)\\\cline{1-3}9&2.2&1.1\\\cline{1-3}20&3.3&1.7\\\cline{1-3}25&3.7&1.9\\\cline{1-3}36&4.5&2.2\\\cline{1-3}64&6.0&3.0\\\cline{1-3}\end{array}`

Explanation:

The logo is composed of a square and two semicircles. When combined, two semicircles form a complete circle. Therefore, the area of the logo is the sum of the area of a square and a circle, where the radius (r) of the circle is equal to half the side length (s) of the square.

`\begin{aligned}\textsf{Area of logo}&=\textsf{Area of a square}+\textsf{Area of a circle}\\&=s^2+\pi r^2\end{aligned}`

`r = (s)/(2)\implies s=2r`

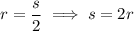
Therefore, the area of the logo expressed in terms of the radius (r) is:

`\begin{aligned}\textsf{Area of logo}&=s^2+\pi r^2\\&=(2r)^2+\pi r^2\\&=4r^2+\pi r^2\\&=(4+\pi)r^2\end{aligned}`

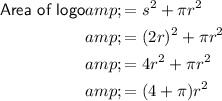
To find the sides of the squares and the radii if the corresponding areas of the logos of different sizes are 9 in², 20 in², 25 in², 36 in² and 64 in², substitute these areas into the area formula and solve for r, then substitute the found value of r into the formula for side length (s).

`\hrulefill`

Logo Area 9 in²

`\begin{aligned}(4+\pi)r^2&=9\\\\r^2&=(9)/(4+\pi)\\\\r&=\sqrt{(9)/(4+\pi)}\\\\r&=1.122596586...\\\\r&=1.1\; \sf in\;(nearest\;tenth)\end{aligned}`

`\begin{aligned}s&=2\cdot \sqrt{(9)/(4+\pi)}\\\\s&=2.24519317...\\\\s&=2.2\; \sf in\;(nearest\;tenth)\end{aligned}`

Therefore, the side length of the square is 2.2 in and the radius of the semicircles is 1.1 in (rounded to the nearest tenth).

`\hrulefill`

Logo Area 20 in²

`\begin{aligned}(4+\pi)r^2&=20\\\\r^2&=(20)/(4+\pi)\\\\r&=\sqrt{(20)/(4+\pi)}\\\\r&=1.6734681...\\\\r&=1.7\; \sf in\;(nearest\;tenth)\end{aligned}`

`\begin{aligned}s&=2\cdot \sqrt{(20)/(4+\pi)}\\\\s&=3.34693637...\\\\s&=3.3\; \sf in\;(nearest\;tenth)\end{aligned}`

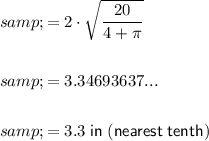
Therefore, the side length of the square is 3.3 in and the radius of the semicircles is 1.7 in (rounded to the nearest tenth).

`\hrulefill`

Logo Area 25 in²

`\begin{aligned}(4+\pi)r^2&=25\\\\r^2&=(25)/(4+\pi)\\\\r&=\sqrt{(25)/(4+\pi)}\\\\r&=1.8709943...\\\\r&=1.9\; \sf in\;(nearest\;tenth)\end{aligned}`

`\begin{aligned}s&=2\cdot \sqrt{(25)/(4+\pi)}\\\\s&=3.74198862...\\\\s&=3.7\; \sf in\;(nearest\;tenth)\end{aligned}`

Therefore, the side length of the square is 3.7 in and the radius of the semicircles is 1.9 in (rounded to the nearest tenth).

`\hrulefill`

Logo Area 36 in²

`\begin{aligned}(4+\pi)r^2&=36\\\\r^2&=(36)/(4+\pi)\\\\r&=\sqrt{(36)/(4+\pi)}\\\\r&=2.24519317...\\\\r&=2.2\; \sf in\;(nearest\;tenth)\end{aligned}`

`\begin{aligned}s&=2\cdot \sqrt{(36)/(4+\pi)}\\\\s&=4.4903863...\\\\s&=4.5\; \sf in\;(nearest\;tenth)\end{aligned}`

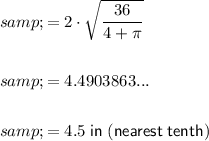
Therefore, the side length of the square is 4.5 in and the radius of the semicircles is 2.2 in (rounded to the nearest tenth).

`\hrulefill`

Logo Area 64 in²

`\begin{aligned}(4+\pi)r^2&=64\\\\r^2&=(64)/(4+\pi)\\\\r&=\sqrt{(64)/(4+\pi)}\\\\r&=2.99359089...\\\\r&=3.0\; \sf in\;(nearest\;tenth)\end{aligned}`

`\begin{aligned}s&=2\cdot \sqrt{(64)/(4+\pi)}\\\\s&=5.98718179...\\\\s&=6.0\; \sf in\;(nearest\;tenth)\end{aligned}`

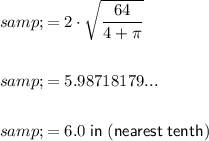
Therefore, the side length of the square is 6.0 in and the radius of the semicircles is 3.0 in (rounded to the nearest tenth).

`\hrulefill`

Solution

Therefore, the completed table is:

`\begin{array}c\cline{1-3}\sf Area\;(in^2)&\sf Side\;(in)&\sf Radius\;(in)\\\cline{1-3}9&2.2&1.1\\\cline{1-3}20&3.3&1.7\\\cline{1-3}25&3.7&1.9\\\cline{1-3}36&4.5&2.2\\\cline{1-3}64&6.0&3.0\\\cline{1-3}\end{array}`

Additional Notes

Please note that the exact value of π has been used in all calculations.

The side lengths of the squares have been calculated using the exact value of the radii.