Question

Ind the equation of the line through the points (−6,4) and (−5,−10).

Enter your answer in slope-intercept form y=mx+b.

Answer 1

y = -14x - 80

Explanation:

use the slope formula to find out the slope first. (y2 - y1) / (x2 - x1)

(-10 - 4) / (-5 + 6) = -14

y = -14x + b

plug in a point on the graph

4 = -14(-6) + b

-80 = b

y = -14x - 80

Answer 2

::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

⋆ Answer:

y = -14x - 80

⋆ Explanation:

Let's solve the problem given to us today! The problem is the following:

⋆ Write the equation for a line passing through (−6,4) and (−5,−10).

So first, I'll start by calculating the slope. The slope of a straight line through two points is given by the formula:

⇒
`\bf{m=\cfrac{y_2-y_1}{x_2-x_1}}`

Substitute the values:

⇒
`\bf{m=\cfrac{-10-4}{-5-(-6)}}`

⇒
`\bf{m=\cfrac{-14}{-5+6}=\cfrac{-14}{1}=-14}`

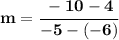
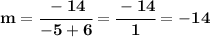
So, the slope is -14. Now, we use the first point (-6,4) and the point-slope formula:

`\Diamond\quad\bf{y-y_1=m(x-x_1)}`

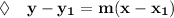
Substitute the values:

`\Diamond\quad\bf{y-4=-14(x-(-6)}`

`\Diamond\quad\bf{y-4=-14(x+6)}`

`\Diamond\quad\bf{y-4=-14x-84}`

`\Diamond\quad\bf{y=-14x-84+4}`

`\Diamond\quad\bf{y=-14x-80}`

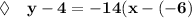
Therefore, the slope-intercept equation of a line that passes through the points (-6,4) and (-5,-10) is y = -14x - 80.

:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::