Question

Please help me!!! work has to be shown as well please and thank you:)

Answer 1

Maximum value = 16

x = 4

y = 0

Explanation:

Given objective function:

`F = 4x + 3y`

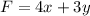
Given constraints:

`\begin{cases}x+3y \leq 6\\x+y\leq 4\\x \geq 0\\y \geq 0\end{cases}`

To find the maximum value of the objective function, we first need to find the corner points of the feasible region, which are the points of intersection of the constraints. These points define the boundaries of the feasible region and represent the potential optimal solutions of the problem.

If we graph the inequalities, we can see that the corner points of the feasible region (the region where all the shaded areas overlap) are the points of intersection of the following boundary lines:

• x = 0 and y = 0
• x = 0 and x + 3y = 6
• x + 3y = 6 and x + y = 4
• y = 0 and x + y = 4

Point 1

When x = 0 and y = 0, the point of intersection is (0, 0).

Point 2

Solve x + 3y = 6 when x = 0:

`\begin{aligned}0+3y&=6\\3y&=6\\y&=2\end{aligned}`

Therefore, the point of intersection is (0, 2).

Point 3

Solve x + 3y = 6 when x + y = 4.

Rewrite the second equation to isolate y, then substitute this into the first equation:

`\begin{aligned}x+3(4-x)&=6\\x+12-3x&=6\\12-2x&=6\\6&=2x\\x&=3\end{aligned}`

Substitute the found value of x into x + y = 4:

`\begin{aligned}3+y&=4\\y&=1\end{aligned}`

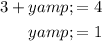
Therefore, the point of intersection is (3, 1).

Point 4

Solve x + y = 4 when y = 0:

`\begin{aligned}x+0&=4\\x&=4\end{aligned}`

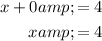
Therefore, the point of intersection is (4, 0).

Therefore, the coordinates of the corner points of the feasible region are:

• (0, 0)
• (0, 2)
• (3, 1)
• (4, 0)

To find the maximum value of the given objective function (subject to the given constraints), evaluate the objective function F = 4x + 3y at each of the corner points:

`\begin{aligned}(0,0)\implies F&=4(0)+3(0)\\F&=0+0\\F&=0\end{aligned}`

`\begin{aligned}(0,2)\implies F&=4(0)+3(2)\\F&=0+6\\F&=6\end{aligned}`

`\begin{aligned}(3,1)\implies F&=4(3)+3(1)\\F&=12+3\\F&=15\end{aligned}`

`\begin{aligned}(4,0)\implies F&=4(4)+3(0)\\F&=16+0\\F&=16\end{aligned}`

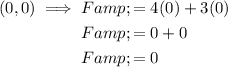
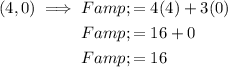
Therefore, the maximum value is 16, and it occurs at point (4, 0).