Question

What is the 50th term of the sequence an = 100 (-8) (n-1)?

Answer 1

The 50th term of the sequence
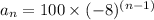`\(a_n = 100 * (-8)^((n-1))\)` is -8,192,000.

Step-by-step explanation:

The sequence
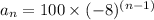`\(a_n = 100 * (-8)^((n-1))\)` represents a geometric sequence where each term is obtained by multiplying the previous term by -8. The formula for the nth term of a geometric sequence is where is the first term, \(r\) is the common ratio, and \(n\) is the term number.

In this sequence, the first term
`\(a_1\)`is given as 100, and the common ratio r is -8. Substituting these values into the formula, we get:

`\(a_(50) = 100 * (-8)^((50-1)) = 100 * (-8)^(49)\)`

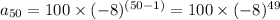
Now, to find the 49th power of -8, we multiply -8 by itself 49 times:

`\((-8)^(49) = -8 * (-8)^(48)\)`

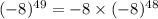
Continuing this process, eventually, we'll get to
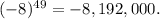`\((-8)^(49) = -8,192,000\).`Thus, the 50th term of the sequence is -8,192,000.

This demonstrates the exponential decrease in the sequence where each term is 8 times smaller than the previous one due to the negative common ratio. The sequence exponentially diminishes toward negative infinity, converging towards zero but never actually reaching it due to the negative multiplication factor. Therefore, the 50th term of the sequence is -8,192,000, showcasing the rapid decrease in magnitude as the terms progress in the sequence.

Answer 2

`\[a_(50) = 100 * (-8)^(50-1)\]`

It looks like there might be a typographical error in the sequence formula you provided. I'll assume you meant
`\(a_n = 100 * (-8)^(n-1)\)`. If that's correct, then this is a geometric sequence where the first term
`(\(a_1\))` is 100 and the common ratio
`(\(r\))` is -8.

The general formula for the
`\(n\)`-th term
`(\(a_n\))` of a geometric sequence is given by:

`\[a_n = a_1 * r^((n-1))\]`

In this case,
`\(a_1 = 100\)` and
`\(r = -8\)`. Plugging these values into the formula, we get:

`\[a_n = 100 * (-8)^(n-1)\]`

Now, to find the 50th term
`(\(a_(50)\))`, substitute
`\(n = 50\)` into the formula:

`\[a_(50) = 100 * (-8)^(50-1)\]`

Calculate this expression to find the 50th term of the sequence. Keep in mind that as
`\(n\)` increases, the terms in the sequence will become very large, and you may end up with a very large negative value due to the negative common ratio.