Answer:

Explanation:
To Multiply:
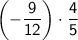
Note:
The product of two numbers is the result of multiplying them together. Multiplication is one of the four basic arithmetic operations, along with addition, subtraction, and division.
Solution:
In this case, the two numbers are
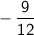 and
and
 .
.
To multiply two fractions, we multiply the numerators and the denominators:
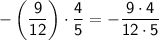
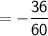
We can simplify the fraction by dividing the numerator and denominator by 12:
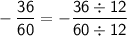
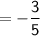
Therefore, the product is:
