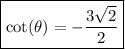Question

I need help! 20 Points for whoever can help me.

Answer 1

`\cot(\theta)=-(3\sqrt2)/(2)`

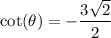
Explanation:

The trigonometric ratio cotangent is defined as:

`\cot(\theta) = (1)/(\tan(\theta)) = (\cos(\theta))/(\sin(\theta))`

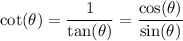
The trigonometric ratios sine and cosine are defined as:

`\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}`

`\cos(\theta)=\frac{\text{adjacent}}{\text{hypotenuse}}`

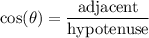
We can identify the following values from the given graph:

• 
  `\text{adjacent}=-6`
• 
  `\text{opposite}=2\sqrt2`

Next, to find sine and cosine, we need to find the hypotenuse, labeled r for radius in the given graph. We can use the Pythagorean Theorem for this:

`a^2 + b^2 = c^2`

↓ plugging in the known values

`\begin{aligned}(-6)^2 + \left(2\sqrt2\,\right)\!^(2) &= r^2\\ 36 + 4(2) &= r^2 \\ 36 + 8 &= r^2\\ 44 &= r^2 \\ √(44) &= r \\ \sqrt4√(11) &= r \\ 2√(11)&=r\end{aligned}`

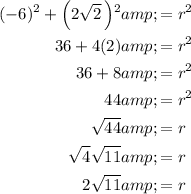
Now that we have the hypotenuse, we can define sine and cosine as:

• 
  `\sin(\theta) = (2\sqrt2)/(2√(11)) = (\sqrt2)/(√(11))`
• 
  `\cos(\theta)=(-6)/(2√(11)) = (-3)/(√(11))`

Finally, using these sine and cosine ratios, we can define cotangent as:

`\cot(\theta) = (\cos(\theta))/(\sin(\theta))`

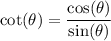
↓ plugging in the known ratios

`\cot(\theta) = ((-3)/(√(11)))/(\,(\sqrt2)/(√(11)))`

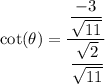
↓ representing division by a fraction as multiplication by its reciprocal

`\cot(\theta) = {\,(-3)/(√(11))} \cdot (√(11))/(\sqrt2)`

↓ canceling the
`√(11)` in the numerator and denominator

`\boxed{\cot(\theta)=-(3)/(\sqrt2)}`

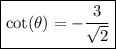
Optionally, we can also rationalize the numerator to meet the form indirectly asked for by the question:

`\cot(\theta)=-(3)/(\sqrt2) \cdot (\sqrt2)/(\sqrt2)`

`\boxed{\cot(\theta)=-(3\sqrt2)/(2)}`