Question

Investments increase exponentially by about 15%

every 2 years. If you start with a $500 investment,
how much money would you have after 40 years?
Future Amount = [ ? ](1 +)^?
Future Amount = I(1 + r)t

Answer 1

$133,931.77

Explanation:

The future amount of an investment can be calculated using the following formula:

`\sf \textsf{ Future Amount } = I(1 + r)^t`

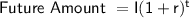
where,

• I is the initial investment amount
• r is the annual interest rate
• t is the number of years

In this case, we have the following information:

• I = $500
• r = 15% = 0.15 in decimal
• t = 40 years

In order to calculate the future amount, we can simply substitute these values into the formula:

`\sf \textsf{ Future Amount } = \$500(1 + 0.15)^(40)`

`\sf \textsf{ Future Amount } = \$500(1.15)^(40)`

`\sf \textsf{ Future Amount } = \$500 \cdot 267.86354623`

`\sf \textsf{ Future Amount } = \$133931.77 \textsf{( in 2 d.p)}`

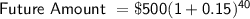
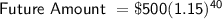
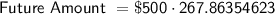
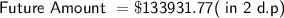
Therefore, after 40 years, our $500 investment would be worth $133,931.77.

Note:

• The future amount of an investment is the value of the investment at a future date, taking into account the interest that will be earned.
• The initial investment amount is the amount of money that is invested initially.
• The annual interest rate is the percentage of the initial investment amount that is earned in interest each year.
• The number of years is the amount of time that the investment is held.