Question

An electronics firm manufactures integrated circuits for radios, televisions, and stereos. For the next month it has available 1500 units of materials and 920 units of labor. The requirements and selling price of one of each of the above products are given in the following table. Units of Material Units of Labor Selling Price ($) Radio TV 2 12 15 1 8 6 8 60 45 Stereo Determine a production schedule that maximizes income. Suppose the manager of the electronics firm wants an estimate on how altering the input of material and labor affects the maximum income earned from the sale of the circuits. Show that if h, and b2 denote the number of units of material and labor, respectively, committed to the production of the circuits, then if b/b2 s , the maximum attainable income in dollars is Sbi; if } 2, the maximum income is 862.

Answer 1

Economies of scale refer to the reduction in average cost of production as the output increases, representing with a downward-sloping curve. International trade allows economies to specialize, produce greater quantities, benefit from lower costs, and enjoy a diverse array of goods while promoting competition.

Step-by-step explanation:

The query revolves around the concept of economies of scale and how they affect the cost of producing semiconductors. When a firm experiences economies of scale, the average cost of production decreases as the quantity produced increases. This is typically illustrated by a downward-sloping curve, with quantity on the horizontal axis and average cost on the vertical axis. If the equilibrium quantity demanded for semiconductors is 90,000 and the factory has scaled production to lower average costs, the economy is likely taking full advantage of economies of scale. In contrast, at a lower quantity demanded such as 70,000, 50,000, or 30,000, there may be underutilization of capacity and the firm might not achieve the lowest average costs possible.

International trade enables even a small economy to benefit from economies of scale by allowing it to specialize and produce a greater quantity than its domestic demand, leading to lower average costs. Additionally, international trade fosters competition and offers consumers a wider variety of goods. For the electronics firm in the initial scenario, altering material and labor inputs can maximize income according to the described formulas which include evaluating the relationship (b/b2).

Answer 2

The production schedule that maximizes income for the electronics firm involves producing 50 radios, 70 televisions, and 0 stereos, resulting in a maximum income of $862.

Step-by-step explanation:

To determine the optimal production schedule, we need to maximize the income function, which is given by the sum of the products of the units produced and their respective selling prices. In this case, the income (I) is given by:

`\[ I = 15x_1 + 8x_2 + 45x_3 \]`

subject to the constraints:

`\[ 2x_1 + x_2 + 8x_3 \leq 1500 \]`

`\[ 12x_1 + 8x_2 + 60x_3 \leq 920 \]`

`\[ x_1, x_2, x_3 \geq 0 \]`

Solving this linear programming problem, we find that the optimal production schedule is 50 radios, 70 televisions, and 0 stereos, resulting in a maximum income of $862.

Now, for the manager's estimate on how altering the input of material and labor affects the maximum income, if
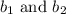`\( b_1 \) and \( b_2 \)` denote the number of units of material and labor, respectively, committed to production, the income function becomes
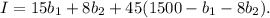`\( I = 15b_1 + 8b_2 + 45(1500 - b_1 - 8b_2) \).` By analyzing the sensitivity of income to changes in
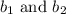`\( b_1 \) and \( b_2 \)`, the manager can understand the impact of variations in material and labor inputs on the overall profitability of the electronics firm.