Question

For x/y+5x−7=−3/4y, (1, 2) , find the equation of the tangent line to the graph of the given equation at the indicated point

Answer 1

The equation of the tangent line to the graph of
`\( (x)/(y) + 5x - 7 = -(3)/(4)y \) at the point (1, 2) is \( y = (3)/(4)x + (5)/(2) \).`

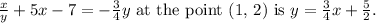
Step-by-step explanation:

To find the equation of the tangent line at the point (1, 2) for the given equation, differentiate the equation implicitly with respect to \( x \) to find the slope of the tangent line. After differentiating and solving for
`\( (dy)/(dx) \),` substitute the given point's coordinates (1, 2) to find the slope.

Next, utilize the point-slope form of a line
`\( y - y_1 = m(x - x_1) \), where \( (x_1, y_1) \) is the point and \( m \)`is the slope. Substitute the slope calculated and the given point (1, 2) into the point-slope form to derive the equation of the tangent line.

The derived equation
`\( y = (3)/(4)x + (5)/(2) \) represents the tangent line to the graph of the given equation \( (x)/(y) + 5x - 7 = -(3)/(4)y \) at the specified point (1, 2).`

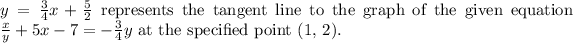
Understanding implicit differentiation and the point-slope form of a line is essential in determining tangent lines to curves at specific points, enabling the accurate depiction of the curve's behavior at those points.