Question

If the area of a rectangle is x² + 15x + 50,

find the length and width of the figure.
Length:
Width:

Answer 1

Length = x + 10

Width = x + 5

Explanation:

The area of a rectangle is the product of its length and width.

Let the length of the rectangle be l and the width be w. We know that the area of the rectangle is x² + 15x + 50, so we can write the following equation:

lw = x² + 15x + 50

We can factor the expression on the right-hand side of the equation as follows:

x² + 15x + 50

Doing middle term factorization:

x²+(10+5)x+50

x²+10x + 5x + 50

Take common from each two terms.

x(x+10)+5(x+10)

Take common and keep remaining in brackets.

(x+5)(x + 10)

Therefore, the length and width of the rectangle are x + 10 and x + 5 respectively.

Answer 2

Length: x + 10

Width: x + 5

Explanation:

Given the area of a rectangle is x² + 15x + 50, to find the expressions for its length and width, we need to factor the quadratic.

To factor a quadratic in the form ax² + bx + c, we need to find two numbers that multiply to ac and sum to b.

In this case:

• a = 1
• b = 15
• c = 50

Therefore, we need to find two numbers that multiply to 50 and sum to 15.

The factors of 50 are 1, 2, 5, 10, 25 and 50. Therefore, the two numbers are 5 and 10.

Rewrite b as the sum of these two numbers:

`x^2+5x+10x+50`

Factor the first two terms and the last two terms separately:

`x(x+5)+10(x+5)`

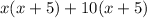
Factor out the common term (x + 5):

`(x+5)(x+10)`

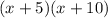
In a rectangle, the length of a rectangle is typically associated with its longer side, while the width is associated with the shorter side.

Therefore, the dimensions of a rectangle with area x² + 15x + 50 are:

• Length: x + 10
• Width: x + 5