Question

(2s+1)x2=s(3x-1)

Find:
1.Two distinct real roots
2.One real repeated root
3.No real roots
Help pls!!!

Answer 1

1. s < 0 or s > 4

2. s = 0, s = 4

3. 0 < s < 4

Explanation:

Begin by simplifying the given equation so that it is in the form ax² + bx + c = 0:

`\begin{aligned}(2s+1)x^2&=s(3x-1)\\(2s+1)x^2&=3sx-s\\(2s+1)x^2-3sx+s&=0\end{aligned}`

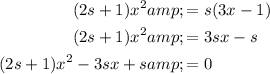
Therefore, the coefficients a, b and c are:

• a = (2s + 1)
• b = -3s
• c = s

The discriminant is defined as the expression b² - 4ac, which appears under the square root sign in the quadratic formula.

The value of the discriminant determines the nature of the solutions to the quadratic equation.

`\boxed{\begin{minipage}{6.8 cm}\underline{Discriminant}\\\\$b^2-4ac$ \quad when $ax^2+bx+c=0$\\\\$b^2-4ac > 0 \implies$ two real roots\\$b^2-4ac=0 \implies$ one real root\\$b^2-4ac < 0 \implies$ no real roots\\\end{minipage}}`

Substitute the values of a, b and c into the discriminant formula:

`\begin{aligned}b^2-4ac&=(-3s)^2-4(2s + 1)s\\&=9s^2-8s^2-4s\\&=s^2-4s\\&=s(s-4)\end{aligned}`

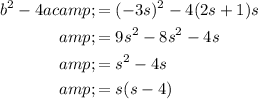
To identify the value of s resulting in two distinct real roots, set the discriminant to greater than zero and solve for s:

`\begin{aligned}s(s-4)& > 0\\\\\implies s& < 0\\\implies s& > 4\end{aligned}`

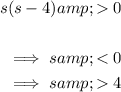
Therefore, the values of s where the quadratic will have two distinct real roots is s < 0 or s > 4.

To identify the value of s resulting in one real repeated root, equate the discriminant to zero and solve for s:

`\begin{aligned}s(s-4)&=0\\\\\implies s&=0\\\implies s&=4\end{aligned}`

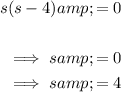
Therefore, the values of s where the quadratic will have one real repeated root is s = 0 and s = 4.

To identify the value of s resulting in no real roots, set the discriminant to less than zero and solve for s:

`\begin{aligned}s(s-4)& < 0\\\\\implies s& > 0\\\implies s& < 4\end{aligned}`

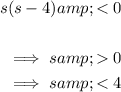
Therefore, the values of s where the quadratic will have no real roots is 0 < s < 4.

Additional Notes

To determine the intervals of "s" for each of the three discriminant expressions, simply graph the discriminant as a function: y = x² - 4x. This is a parabola that opens upwards and crosses the x-axis (equal to zero) at x = 0 and x = 4. It is above the x-axis (greater than zero) when x < 0 and x > 4, and below the x-axis (less than zero) when 0 < x < 4.