Final Answer:1.
The polynomial
 can be rewritten using the distributive property as
can be rewritten using the distributive property as
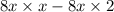
Step-by-step explanation:
To rewrite the given polynomial
 using the distributive property, we distribute each term in the first parenthesis to each term in the second parenthesis.
using the distributive property, we distribute each term in the first parenthesis to each term in the second parenthesis.
The distributive property is expressed as
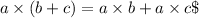 ). Applying this to the given polynomial, we distribute
). Applying this to the given polynomial, we distribute
 an
an

The first term becomes
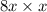 and the second term becomes
and the second term becomes
 . Combining these results, the rewritten polynomial is
. Combining these results, the rewritten polynomial is

Further simplifying,
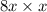 is
is
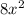 , and
, and
 is -16x Therefore, the final expression is
is -16x Therefore, the final expression is
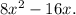
In summary, using the distributive property, we expanded the given polynomial by multiplying each term in the first set of parentheses with each term in the second set. The final result is
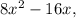 which is the rewritten form of the original polynomial.
which is the rewritten form of the original polynomial.