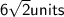Answer:
Explanation:
A diagonal in a square is a line segment that joins two non-adjacent vertices of the square. A square has two diagonals, and they are both equal in length and perpendicular to each other.
In order to find length of diagonal let's take any diagonal points (0,6) and (6,0) or (0,0) and (6,6).
I will choose coordinate (0,0) and (6,6).
Now.
Using distance formula:
The distance formula is used to calculate the distance between two points in a coordinate plane. The formula is as follows:

where:
(x1, y1) and (x2, y2) are the coordinates of the two points
In this case, we are calculating the distance between the points (0, 0) and (6, 6).
Substituting these values into the distance formula, we get:


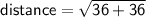
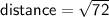
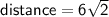
Therefore, length of one of the diagonals of the square is