Question

Write an equation of a line perpendicular to y=1/4x + 13 and contains P(4,7)

a. in point slope form
b. in slope intercept form
c.name another point on the line

Answer 1

a) y - 7 = -4(x - 4)

b) y = -4x + 23

c) (0, 23)

Explanation:

The slope of the line y=¼ x + 13 is ¼. The slope of a perpendicular line is the negative reciprocal of the original slope, so the slope of the perpendicular line is -4.

Point-Slope Form:

To find the equation of the perpendicular line in point-slope form, we can use the following formula:

`\sf y - y_1 = m(x - x_1)`

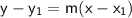
where:

(x1, y1) is a point on the line

m is the slope of the line

We know that the perpendicular line contains the point P(4, 7) and has a slope of -4.

Substitute these values into the formula, we get:

y - 7 = -4(x - 4)

This is the equation of the perpendicular line in point-slope form.

Slope-Intercept Form:

To convert the equation to slope-intercept form, we can distribute the -4 on the right-hand side of the equation and solve for y:

y - 7 = -4x + 16

y = -4x + 16 + 7

y = -4x + 23

This is the equation of the perpendicular line in slope-intercept form.

Another Point on the Line:

To find another point on the line, we can plug any x-value into the equation and solve for y.

For example, if we plug in x = 0, we get:

y = -4(0) + 23

y = 23

Therefore, another point on the line is (0, 23).

Answer 2

see explanation

Explanation:

(a)

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

y =
`(1)/(4)` x + 13 ← is in slope- intercept form

with slope m =
`(1)/(4)`

given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/((1)/(4) )` = - 4

the equation of a line in point- slope form is

y - b = m(x - a)

m is the slope and (a, b ) a point on the line

here m = - 4 and (a, b ) = P (4, 7 ) , then

y - 7 = - 4(x - 4) ← equation in point- slope form

(b)

point- slope form of the equation is

y - 7 = - 4(x - 4) ← distribute parenthesis by - 4

y - 7 = - 4x + 16 ( add 7 to both sides )

y = - 4x + 23 ← equation in slope- intercept form

(c)

y = - 4x + 23

the y- intercept is c = 23

then (0, 23 ) ← is another point on the line