Question

Center is at (−3,4) and through the point (2,0).

Answer 1

Answer:
`(x+3)^(2) +(y-4)^2=41`

Explanation:

Is is a circle? If then the radius is
`√((2--3)^2+(0-4)^2)`=
`√(5^2+4^2)=√(41)`

The equation of the circle would be
`(x+3)^(2) +(y-4)^2=41`

Answer 2

`(x+3)^2+(y-4)^2=41`

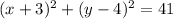
Explanation:

The equation of a circle is:

`\large\boxed{(x-h)^2+(y-h)^2=r^2}`

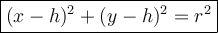
where:

• (h, k) is the center.
• r is the radius.

Given the center of the circle is (-3, 4):

• h = -3
• k = 4

Therefore:

`(x-(-3))^2+(y-4)^2=r^2`

`(x+3)^2+(y-4)^2=r^2`

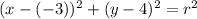
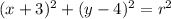
To find the value of r², substitute point (2, 0) into the equation:

`\begin{aligned}(2+3)^2+(0-4)^2&=r^2\\(5)^2+(-4)^2&=r^2\\25+16&=r^2\\41&=r^2\end{aligned}`

Therefore, the equation of the circle with center (-3, 4) and passing through the point (2, 0) is:

`\large\boxed{\boxed{(x+3)^2+(y-4)^2=41}}`