Question

You purchase a $142.83 ticket for your favorite band. You remember your dad mentioning how much tickets cost now compared to when he was a kid. If you are 17, how much will concert tickets cost when you are twice as old as you are now, assuming inflation is compounding continuously at a rate of 9.32%?

Answer 1

$696.49

Explanation:

In order to calculate how much concert tickets will cost when you are twice as old as we are now, assuming inflation is compounding continuously at a rate of 9.32%, we can use the following formula:

`\sf \textsf{Future value = Present value } * e^{(\textsf{inflation rate} * time)}`

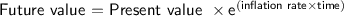
where:

• Future value is the value of the investment in the future
• Present value is the value of the investment today
• Inflation rate is the annual inflation rate
• Time is the number of years until the future value is needed

In this case, the present value is $142.83, the inflation rate is 9.32% (0.0932 in decimal), and the time is 17 years (because you are 17 years old now and we want to know how much tickets will cost when we are twice as old, which is 17 × 2 = 34 years old).

Substitute these values into the formula, we get:

`\sf \textsf{Future value }= \$ 142.83 * e^(0.0932 * 17)`

`\sf \textsf{Future value }= \$ 142.83 * e^(1.5844)`

`\sf \textsf{Future value }= \$ 696.49 \textsf{ in 2 d.p}`

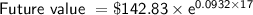
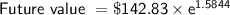
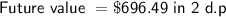
Therefore, concert tickets will cost $696.49 when we are twice as old as we are now, assuming inflation is continuously compounding at a rate of 9.32%.