Question

Three forces act on the ring. Determine the magnitude and coordinate direction angles of the resultant force.

Answer 1

Magnitude of Resultant Force is:

`\[ F_R = \sqrt{F_(Rx)^2 + F_(Ry)^2 + F_(Rz)^2} \]`

Coordinate Direction Angles are:

`\[ \cos(\alpha) = (F_(Rx))/(F_R) \]`

`\[ \cos(\beta) = (F_(Ry))/(F_R) \]`

`\[ \cos(\gamma) = (F_(Rz))/(F_R) \]`

To determine the magnitude and coordinate direction angles of the resultant force when three forces act on a ring, you would typically follow these steps:

1. Vector Representation: Express each force in vector form, with components along the x, y, and z axes (if in three dimensions).

2. Summation of Components: Sum the components of all the forces along each axis to find the components of the resultant force:

`\[ F_(Rx) = F_(1x) + F_(2x) + F_(3x) \]`

`\[ F_(Ry) = F_(1y) + F_(2y) + F_(3y) \]`

`\[ F_(Rz) = F_(1z) + F_(2z) + F_(3z) \]`

(The z-components are only needed if there are forces acting in three dimensions.)

3. Magnitude of Resultant Force: Calculate the magnitude of the resultant force using the Pythagorean theorem:

`\[ F_R = \sqrt{F_(Rx)^2 + F_(Ry)^2 + F_(Rz)^2} \]`

(If only in two dimensions, omit the z-components.)

4. Coordinate Direction Angles: Calculate the coordinate direction angles
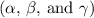`(\( \alpha \), \( \beta \), and \( \gamma \))`with respect to the x, y, and z axes using the following formulas:

`\[ \cos(\alpha) = (F_(Rx))/(F_R) \]`

`\[ \cos(\beta) = (F_(Ry))/(F_R) \]`

`\[ \cos(\gamma) = (F_(Rz))/(F_R) \]`

Then solve for the angles
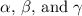`\( \alpha \), \( \beta \), and \( \gamma \)`usually using the inverse cosine function.

5. Verifying: Ensure that the cosines of the direction angles add up to 1 when squared and summed, as a check on the calculations:

`\[ \cos^2(\alpha) + \cos^2(\beta) + \cos^2(\gamma) = 1 \]`