Question

Having difficulty solving this one

Answer 1

`\sf y = (1)/(2)x -2`

Explanation:

Before finding the equation for the graph. let's take two points from the graph in which the line passes.

I took a point (-2,-3) and (2,-1).

Now,

The equation for the line that passes through the points (-2, -3) and (2, -1) can be found using the following steps:

Calculate the slope of the line using the slope formula:

`\sf slope = (y_2 - y_1)/(x_2 - x_1)`

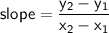
Substitute the value:

tex]\sf slope = \dfrac{-1- (-3)}2 - (-2)}=\dfrac{2}{4}=\dfrac{1}{2}[/tex]

Use the point-slope form of the equation of a line to find the equation of the line, which is:

`\sf y - y_1 = m(x - x_1)`

`\sf y - (-3) = (1)/(2)(x - (-2))`

`\sf y + 3 = (1)/(2)x + 1`

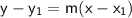
Simplify the equation by combining like terms:

`\sf y = (1)/(2)x + 1-3`

`\sf y = (1)/(2)x -2`

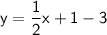
Therefore, the equation for the line that passes through the points (-2, -3) and (2, -1) is:

`\sf y = (1)/(2)x -2`

Definition: The equation of a line is the mathematical expression that represents the relationship between the x and y coordinates of any point on the line.

Answer 2

y =
`(1)/(2)` x - 2

Explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

calculate m using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

let (x₁, y₁ ) = (- 2, - 3) and (x₂, y₂ ) = (2, - 1) ← 2 points on the line

substitute these values into the formula for m

m =
`(-1-(-3))/(2-(-2))` =
`(-1+3)/(2+2)` =
`(2)/(4)` =
`(1)/(2)`

the line crosses the y- axis at (0, - 2 ) so y- intercept c = - 2

y =
`(1)/(2)` x - 2 ← equation of line