Answer:
Approximately
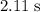 , assuming that air resistance is negligible and that
, assuming that air resistance is negligible and that
 .
.
Step-by-step explanation:
Under the assumptions, this person would be accelerating downward at a constant
 until reaching the water. Note that acceleration is negative since gravitational attraction points downwards.
until reaching the water. Note that acceleration is negative since gravitational attraction points downwards.
Initial velocity of this person would be
 - positive since this person was initially moving upward. The displacement during the entire motion would be
- positive since this person was initially moving upward. The displacement during the entire motion would be
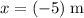 , which is negative since the water is below the initial position of the diving board.
, which is negative since the water is below the initial position of the diving board.
The duration of this motion can be found in the following steps:
- Apply the SUVAT equation
 to find the velocity
to find the velocity
 of the person right before hitting the water.
of the person right before hitting the water. - Divide the change in velocity by acceleration (the rate of change in velocity) to find the duration of the motion.
In the SUVAT equation
 :
:
 is the final velocity of the object,
is the final velocity of the object,
 is the initial velocity of the object,
is the initial velocity of the object,
 is acceleration, and
is acceleration, and
 is the displacement of the object.
is the displacement of the object.
Rearrange this equation to find
 given that
given that
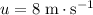 ,
,
 , and
, and
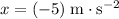 :
:
 .
.
Note that two different values of
 that would satisfy this equation: one positive, and the other negative. However, since the diver would be travelling downward right before hitting the water, the correct value of
that would satisfy this equation: one positive, and the other negative. However, since the diver would be travelling downward right before hitting the water, the correct value of
 should be negative. Hence, there should be a negative sign in front of the square root:
should be negative. Hence, there should be a negative sign in front of the square root:
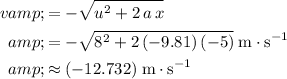 .
.
In other words, the velocity of this person would be approximately
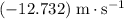 right before reaching the water.
right before reaching the water.
Velocity of this person has changed from
 to
to
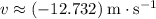 . Divide the change in velocity by the acceleration (the rate of change in velocity) to find the duration of this motion:
. Divide the change in velocity by the acceleration (the rate of change in velocity) to find the duration of this motion:
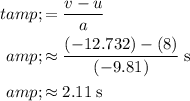 .
.
In other words, this person was in the air for approximately
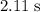 .
.