Question

Helpp meeee with question 2 and 1

Answer 1

`\begin{aligned}\textsf{2)}\quad &-3i\\&4 + 5i\end{aligned}`

`\textsf{3)} \quad (3)/(17)+(22)/(17)i`

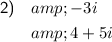
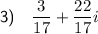
Explanation:

A complex number is a number that can be expressed in the form
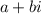`a + bi`, where "a" and "b" are real numbers, and "i" represents the imaginary unit with the property that i² = -1.

The complex conjugate of a complex number is formed by changing the sign of its imaginary part while keeping the real part unchanged. Therefore, for any complex number
`z=a+bi`, the complex conjugate of the number is defined as
`z^*=a-bi`.

`\hrulefill`

Question 2

The complex number 3i is the equivalent of 0 + 3i.

Therefore, its complex conjugate is 0 - 3i = -3i.

The complex conjugate of 4 - 5i is 4 + 5i.

`\hrulefill`

Question 3

To divide (2 + 5i) by (4 - i), multiply both the numerator and denominator by the complex conjugate of the denominator (4 + i) to eliminate the imaginary part in the denominator:

`\begin{aligned}(2+5i)/(4-i)&=((2+5i)(4+i))/((4-i)(4+i))\\\\&=(8+2i+20i+5i^2)/(16+4i-4i-i^2)\\\\&=(8+22i+5(-1))/(16-(-1))\\\\&=(8+22i-5)/(16+1)\\\\&=(3+22i)/(17)\\\\&=(3)/(17)+(22)/(17)i\end{aligned}`

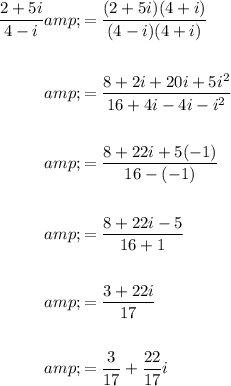
Therefore, the quotient is:

`\large\boxed{\boxed{(3)/(17)+(22)/(17)i}}`