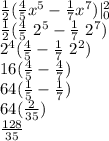Answer:
a)
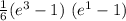
b)
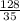
Explanation:
a)
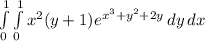
Inside integral is relative to y, so treat x as constant. We can pull x² out of the integral:
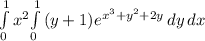
Multiply and divide inside integral by 2:
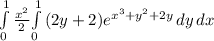
Use identity ∫ eᵘ du = eᵘ.
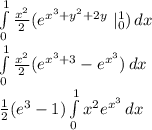
Multiply and divide by 3.
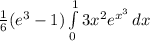
Use same identity as before:
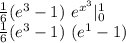
b)
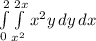
Inside integral is relative to y, so treat x as constant. Pull x² out of inner integral:
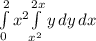
Integrate:
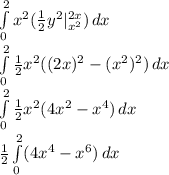
Integrate again: