Question

A uniform beam of laser light has a circular cross-section of diameter d = 5.5 mm. The beam's power is P = 4.8 mW. What is the intensity of the laser beam? Option 1: 2.19 x 10^3 W/m^2 Option 2: 1.09 x 10^3 W/m^2 Option 3: 1.36 x 10^3 W/m^2 Option 4: 5.78 x 10^3 W/m^2

Answer 1

The intensity of the laser beam is approximately 1.36 x 1
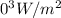`0^3 W/m^2`. Thus the correct option is Option 3. 1.36 x 1
`0^3 W/m^2`.

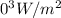Step-by-step explanation:

The intensity (I) of a laser beam can be calculated using the formula:

`\[I = (P)/(A),\]`

where
`\(P\)` is the power of the laser beam and
`\(A\)` is the cross-sectional area of the beam. The cross-sectional area of a circular beam is given by:

`\[A = (\pi \cdot d^2)/(4),\]`

where
`\(d\)` is the diameter of the circular cross-section.

In this case, the diameter of the circular cross-section is given as
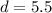`\(d = 5.5\)`mm. First, convert the diameter to meters by dividing it by 1000:
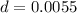`\(d = 0.0055\)` m. Now, substitute this value into the area formula:

`\[A = (\pi \cdot (0.0055)^2)/(4).\]`

Next, use the formula for intensity by substituting the given power
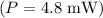`(\(P = 4.8\) mW)` and the calculated area into the intensity formula:

`\[I = (4.8 * 10^(-3))/((\pi \cdot (0.0055)^2)/(4)).\]`

Solving this expression yields the intensity of the laser beam. The final result is approximately
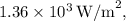`\(1.36 * 10^3 \, \text{W/m}^2\),` matching Option 3.

In summary, the intensity of the laser beam is calculated using the power and cross-sectional area formulas, with the final result falling in line with Option 3.

Thus the correct option is Option 3. 1.36 x 1
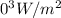`0^3 W/m^2`.